Month: May 2020

29 May

Template for self-assessment questions

GeoGebra 0 Comments

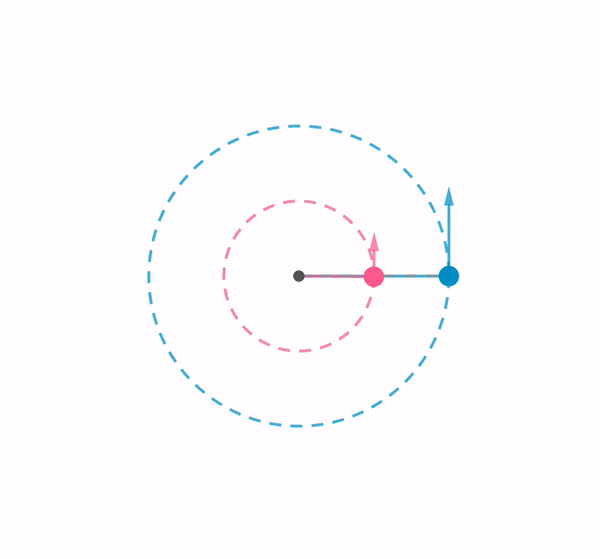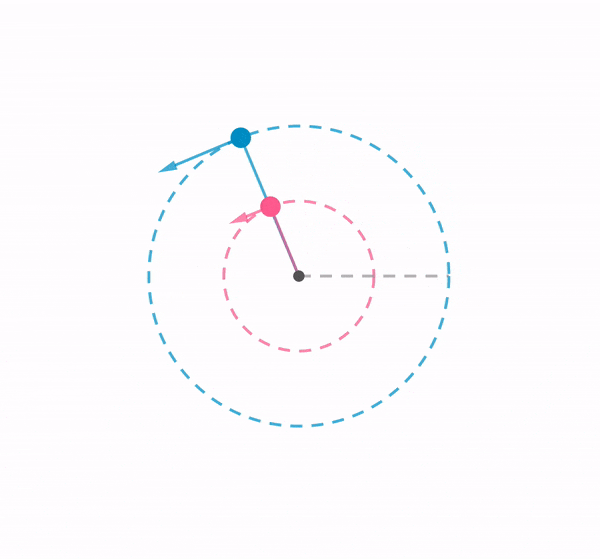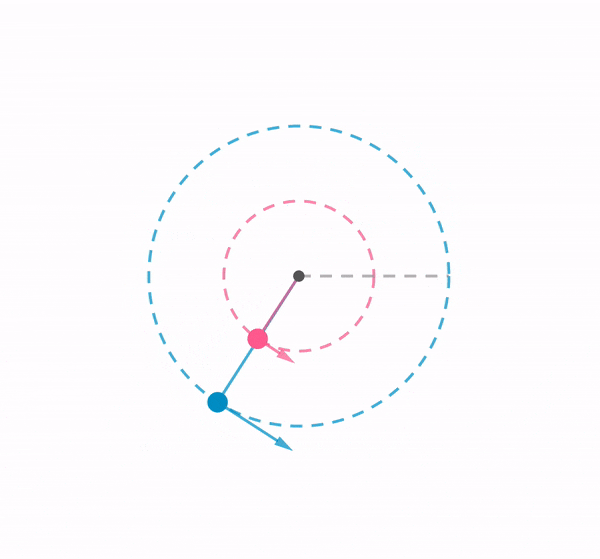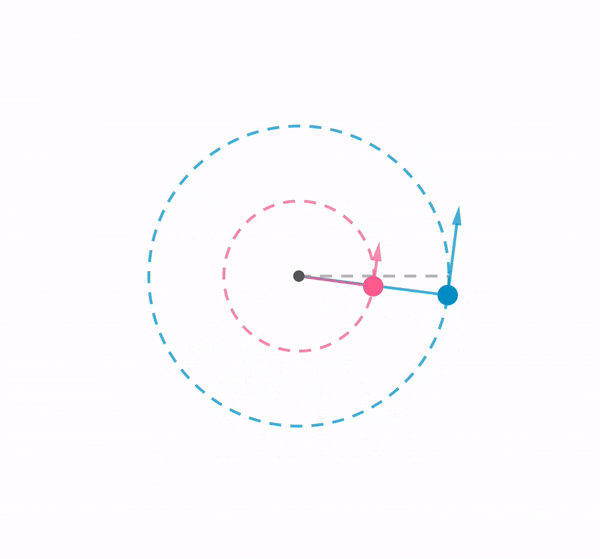
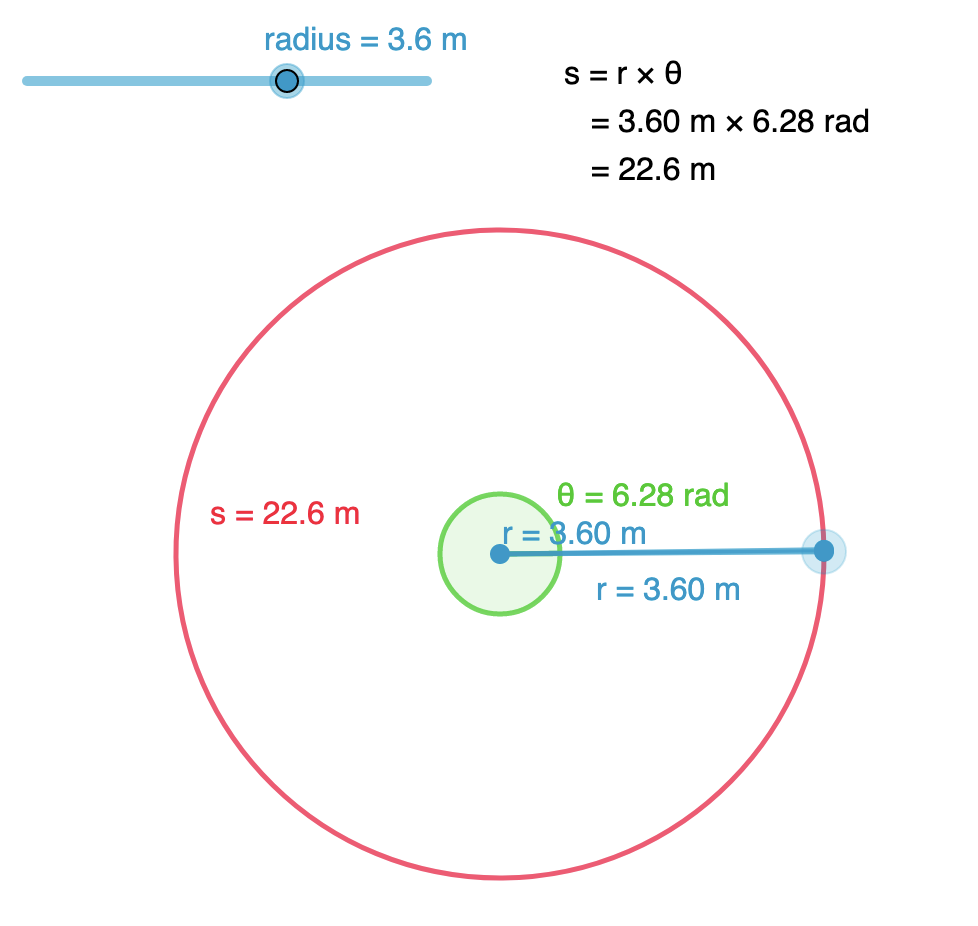
Here is a template that I might use to generate questions for students’ self-assessment in future. Based on a query that one of the participants in a GeoGebra online tutorial asked about generating random questions for simple multiplication for lower primary students.

The online tutorial was conducted by some teachers in the Singapore MOE GeoGebra community to share how GeoGebra could be used to create resources for home-based learning.

27 May

Teaching Python

Programming, Python, Technology 0 Comments

An ex-colleague from HQ introduced me to Trinket: a useful web-based code editor that allows students to tinker with codes and showcase their work. Here’s an example of a BMI calculator that can be embedded via iframes.

As I am teaching programming to the lower sec IP students this term as part of their Skills and Knowledge curriculum, I was wondering if I should use this to ask my students to submit their work.

24 May

Angular velocity

06 Motion in a Circle, GeoGebra 0 Comments

This GeoGebra app shows how angular velocity ω is the rate of change of angular displacement (i.e. $\omega=\dfrac{\theta}{t}$) and is dependent on the speed and radius of the object in circular motion (i.e. $v=r\omega$).

Students can explore the relationships by doing the following:

Keeping r constant and varying ω.

Keeping ω constant and varying r.

Keeping v constant by varying r and ω.

24 May

Angular displacement

06 Motion in a Circle, GeoGebra 0 Comments

This GeoGebra app shows the relationship s = rθ.

One activity I get students can do is to look at the value of θ when the arc length s is equal to the radius r. This would give the definition of the radian, which is the angle subtended at the centre of a circle by an arc equal in length to its radius.

Mathematics defines the constant π as the ratio of a circle’s circumference to its diameter. This can also be shown in the app, although you need to drag the moving point to a point just short of one full revolution.

08 May

Creating a simple interactive using GeoGebra

Seng Kwang Tan GeoGebra 0 Comments

While preparing to share with some fellow teachers in Singapore about the use of GeoGebra in Physics, I came up with a set of simple instructions to create an interactive, while introducing tools such as sliders, checkboxes (along with boolean values) and input boxes. Download it here.

You should be able to follow the instructions in the pdf document above and make a simple interactive applet yourself too. The outcome of the interactive applet will be like this: