Seng Kwang Tan

28 April

Tensegrity Explained

Seng Kwang Tan 04 Forces, Demonstrations, IP3 04 Forces, Lego 1 Comment

There is a new internet trend called “tensegrity” – an amalgamation of the words tension and integrity. It is basically a trend of videos showing how objects appear to float above a structure while experiencing tensions that appear to pull parts of the floating object downwards.

In the diagram below, the red vectors show the tensions acting on the “floating” object while the green vector shows the weight of the object.

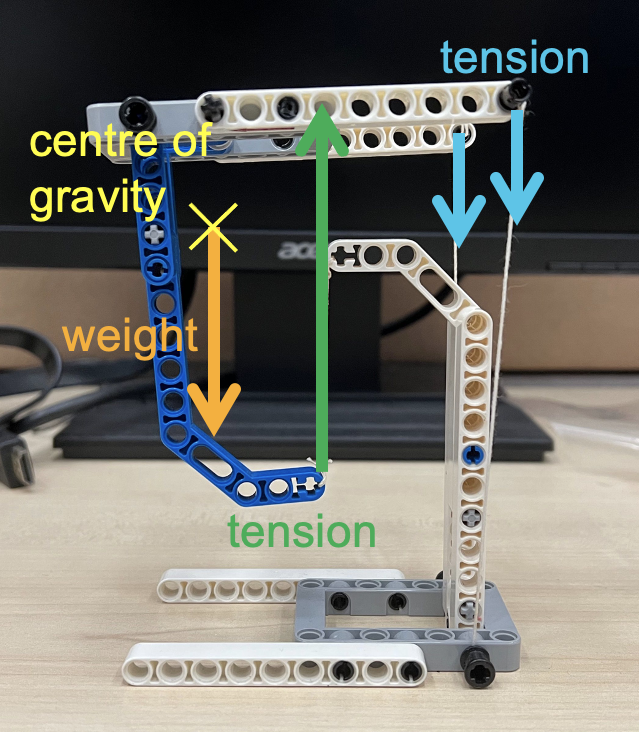
The main force that makes this possible is the upward tension (shown below) exerted by the string from which the lowest point of the object is suspended. The other tensions are downward and serve to balance the moment created by the weight of the object. The centre of gravity of the “floating” structure lies just in front of the supporting string. The two smaller downward vectors at the back due to the strings balance the moment due to the weight, and give the structure stability sideways.

This is a fun demonstration to teach the principle of moments, and concepts of equilibrium.

The next image labels the forces acting on the upper structure. Notice that the centre of gravity lies somewhere in empty space due to its shape.

Only the forces acting on the upper half of the structure are drawn in this image to illustrate why it is able to remain in equilibrium

These tensegrity structures are very easy to build if you understand the physics behind them. Some tips on building such structures:

  1. Make the two strings exerting the downward tensions are easy to adjust by using technic pins to stick them into bricks with holes. You can simply pull to release more string in order to achieve the right balance.
  2. The two strings should be sufficiently far apart to prevent the floating structure from tilting too easily to the side.
  3. The centre of gravity of the floating structure must be in front of the string exerting the upward tension.
  4. The base must be wide enough to provide some stability so that the whole structure does not topple.

Here’s another tensegrity structure that I built: this time, with a Lego construction theme.

Apart from using Lego, I have also 3D-printed a tensegrity structure that only requires rubber bands to hold up. In this case, the centre of gravity of the upper structure is somewhere more central with respect to the base structure. Hence, 3 rubber bands of almost equal tension will be used to provide the balance. The STL file for the 3D model can be downloaded from Thingiverse.com.

The main challenge in assembling a tensegrity structure is the adjustment of the tensions such that the upper structure is balanced. One way to simplify that, for beginners, is to use one that is supported by rubber bands as the rubber bands can adjust their lengths according to the tensions required.

3D-printed tensegrity table balanced by rubber bands

Another tip is to use some blu-tack instead of tying the knots dead such as in the photo below. This is a 3D printed structure, also from Thingiverse.

3D-printed tensegrity table held up and balanced by nylon string

(This post was first published on 18 April 2020 and is revised on 24 August 2022.)

07 October

Pythagorean Cup

Seng Kwang Tan 3D Printing, IP3 05 Density and Pressure, Pressure 0 Comments

This is a 3D printed Pythagorean cup, otherwise known as a greedy cup, where if one pours far too much water or wine or whatever your greedy heart desires, all the contents in the cup will leak out through the bottom.

This is based on the design by “jsteuben” on Thingiverse (https://www.thingiverse.com/thing:123252). The siphoning effect kicks in when the water level is above the internal “tube” printed and hidden into the walls of the cup.

I printed another cup based on a more conventional design as well, but due to the wrong settings given when I prepared the gcode file, the cup was rather leaky when the water level was low. This design by “MonzaMakers” has a protruding siphon tube. (https://www.thingiverse.com/thing:562790)

Explaining how the siphon works is easier with the second cup. When the water level is lower than the highest point in the siphoning tube, it remains in the cup. When it exceeds the highest point of the tube, water begins to flow down the part of the tube leading to the opening at the bottom of the cup. The falling water column creates a suction effect and continuously draws the rest of the water in, until the cup is dry.

21 September

3D Printed Tippe Top

Seng Kwang Tan 3D Printing 0 Comments

After setting up my newest toy, the Creality Ender 3 V2 3D Printer, I started with a few simple prints from the Thingiverse website. The first Physics-related object created is for a colleague – a tippe top. This interesting mushroom-shaped toy is spun with the round top facing down. If it is spun fast enough, it will eventually spin upright, in the opposite orientation to where it started spinning. In doing so, it’s centre of mass even shifted upwards.

The source of the STL file is: https://www.thingiverse.com/thing:536377

The following video gives an explanation for why this happens.

06 September

Pendulum-Powered Car

Seng Kwang Tan 03 Dynamics, 10 Oscillations, Lego 0 Comments

This pendulum-powered car is constructed using Lego Technic parts. I used mainly Lego beams to create the chassis and an “A” frame from which the pendulum is suspended. The pendulum is made of Lego beams and some wheels.

When the pendulum swings, it experiences an acceleration towards its equilibrium position. By the principle of conservation of momentum, the car experiences a change in momentum in the opposite direction. Since the acceleration of the pendulum changes its direction every half a cycle of its oscillation, the car will only oscillate about its original position if the wheels of the car are free to turn throughout the oscillation. 

A escapement mechanism which consists of a beam resting on a pair of 40-tooth gears attached to the front wheels prevent the wheels from rotating in the opposite direction. This means that the car will only be moving forward during the half of the pendulum’s oscillation when its displacement is at the front of its equilibrium position and pauses during the other half.

26 August

Phase Difference

Seng Kwang Tan 11 Wave Motion, GeoGebra 4 Comments

The first of two apps on Phase Difference allows for interaction to demonstrate the oscillation of two different particles along the same wave with a variable phase difference.

The second shows two waves also with a phase difference.

In both cases, the phase difference $\Delta\phi$ can be calculated with

$$\Delta\phi = \dfrac{\Delta x}{\lambda} \times 2\pi$$

where $\Delta x$ is the horizontal distance between the two particles or the horizontal distance between the two adjacent identical particles (one from each wave) and $\lambda$ is the wavelength of the waves.