Here’s a good explanation by Veritasium on why the image of the black hole looks the way it does.
Useful Links for Learning about using GeoGebra in SLS.
- Instructions on how to embed GeoGebra into SLS via iframe (recommended) (Method 1).
- Instructions on how to upload GeoGebra into SLS as a standalone package (Method 2).
- GeoGebra apps curated for A-level Physics: https://www.geogebra.org/m/dgedzmz3
- GeoGebra apps curated for O-level Physics: https://www.geogebra.org/m/z5nfs8qd
- Using GeoGebra Group as an LMS.
- IPSG Poster on “An SLS Learning Experience with GeoGebra Apps on the First Law of Thermodynamics”. Update on 2 Jul 2019: The SLS lesson shared during IPSG 2019 can now be found in the SLS Community Gallery.
- Let us know if you have used or adapted the SLS lesson, or if you have ideas for new GeoGebra apps in the comment section below.
I created a new GeoGebra app based on an ideal Stirling Cycle (A. Romanelli Alternative thermodynamic cycle for the Stirling machine, American Journal of Physics 85, 926 (2017)) which includes two isothermal and two isochoric processes. The Stirling engine is a very good example to apply the First Law of Thermodynamics to, as the amount of gas is fixed so the macro-variables are only pressure, temperature and volume. Simplifying the cycle makes it even easier for first time learners to understand how the engine works.
For those who prefer to be impressed by an actual working model, it can be bought for less than S$30 on Lazada. All you need for it to run is a little hot water or some ice. Here’s a video of the one I bought:
The parts of the Stirling engine are labelled here:

My simulation may not look identical to the engine shown but it does have the same power piston (to do work on the flywheel) and displacer piston (to shunt the air to and fro for more efficient heat exchange).
Geogebra link: https://www.geogebra.org/m/pbnw2yas
Teachers in Singapore have been provided with the Student Learning Space (SLS) – an online platform meant for students’ self-directed learning using MOE’s curriculum-aligned resources as well as for teachers to create engaging technology-assisted learning experiences for their charges.
One of the features that many science and math teachers find useful is the ability to create links out to simulations and other interactive apps. Those who know how can also embed html5 packages into their “Lesson” so as to provide a more seamless experience for their students. These packages must be stand-alone packages that do not require external sources such as sound files or images. In other words, every media file that is needed for the html5 package to run must be all zipped up into a folder before uploading.
Here, I will go through step-by-step how to embed a GeoGebra app into SLS. There are two main methods:
Method 1 is to embed the GeoGebra app in an iframe in SLS using the “Embed Website” method. This is my favourite method as any updates or improvements that I made later to the GeoGebra app is “live” and automatically seen by students when they next log in. It also reduces the AWS load on SLS, thus saving SLS some money. (Same thing for videos, embed as Youtube inside of uploading into SLS if you can help it).
For instructions on how to perform method 1, visit the SLS user guide page found here.
Method 2 is by uploading a GeoGebra package as a zip folder. This means any changes made in GeoGebra after that will not be reflected in the SLS interactive.
Step 1: Find a suitable GeoGebra App (https://www.geogebra.org)
You might like to check out the list of GeoGebra apps that I’ve curated for Singapore’s O-level and A-level syllabi.
Step 2: Open the App and click to see Details.
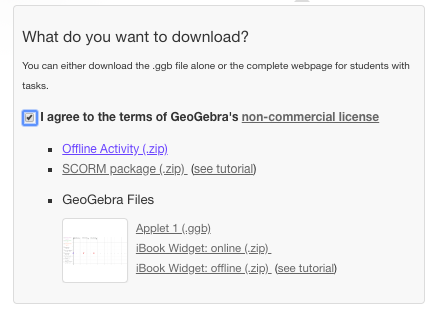
Step 3: Download the App. Be sure to download the version that says “Offline Activity (.zip)”
Step 4: Unzip the package and rename the html file to index.html.
What the file name looks like before:

What the file name should look like after:

Step 4: Zip up the files again. Select all the files including the index.html file and zip it up. Do not zip the main folder. Select only the index.html and the folder with the title GeoGebra. The index.html file must be in the root directory of the new zip folder.

The new zip folder could be given any name.

Step 5: In SLS, select the Lesson and Activity in which you want your GeoGebra app to appear
Step 6: Select a new “Media” object
Step 7: Click Upload
Step 8: Browse to find the zip folder
Step 9: Uploading may take a short while
You should see this message. That is a sign that your package is correctly packaged.

Finally, you can try out the app in the student view.
If you need any assistance, feel free to leave a comment below. I will try my best to support you. In the worst case scenario, I can create the SLS lesson with the desired GeoGebra app and share it with you.
GeoGebra link: https://www.geogebra.org/m/hscshcj8
This simulation demonstrates the power dissipated in a variable resistor given that the battery has an internal resistance (made variable in this app as well).
Since the power dissipated by the resistor is given by
[latex]P=I^2R[/latex]
and the current is given by
[latex]I=E(R+r)[/latex],
[latex]P=E^2\times\dfrac{R}{(R+r)^2}=\dfrac{E^2}{\dfrac{r^2}{R}+R+2r}[/latex]
This power will be a maximum if the expression for the denominator [latex]\dfrac{r^2}{R}+R+2r[/latex] is a minimum.
Differentiating the expression with respect to R, we get
[latex]\dfrac{d(\dfrac{r^2}{R}+R+2r)}{dR}=-\dfrac{r^2}{R^2}+1[/latex]
When the denominator is a minimum,
[latex]-\dfrac{r^2}{R^2}+1=0[/latex]
Therefore,
[latex]r=R[/latex] when the power dissipated by the resistor is highest.
Some of the more challenging problems in the topic of electricity in the A-level syllabus are those involving a potentiometer. The solution involves the concept of potential divider and the setup can be used to measure emf or potential difference across a variety of circuits components. Basically, students need to understand the rule – that the potential difference across a device is simply a fraction of the circuit’s emf, and that fraction is equal to the resistance of the device over the total resistance of the circuit.
[latex]V_{device}=\frac{R_{device}}{R_{total}}*emf[/latex]
The intention of this Geogebra app is for students to practise working on their calculations, as well as to reinforce their understanding of the principle by which the potentiometer works.
GeoGebra link: https://www.geogebra.org/m/pzy3qua8