Seng Kwang Tan

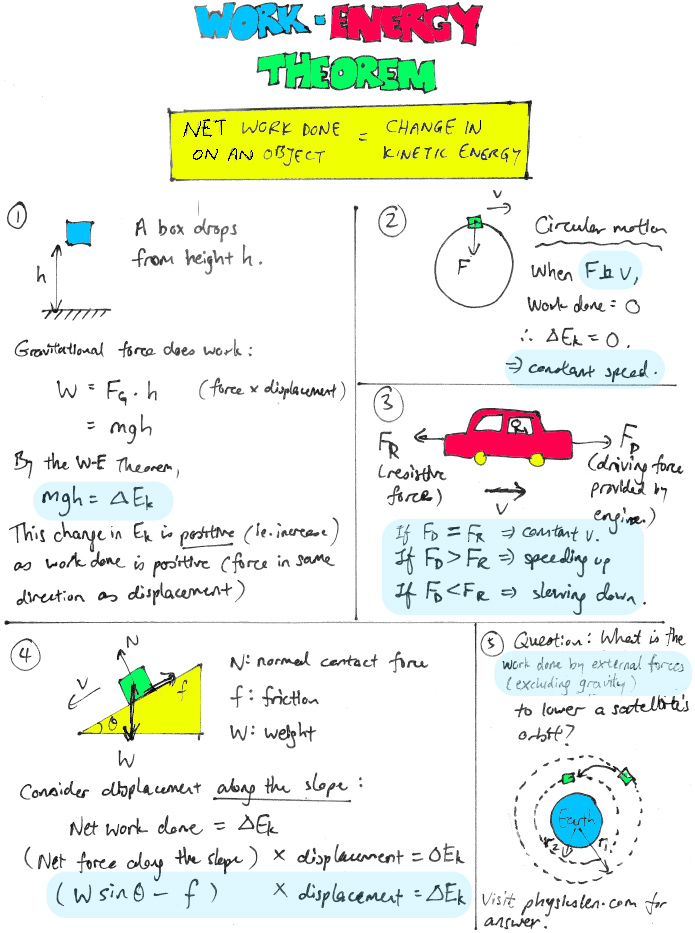
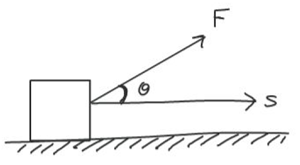
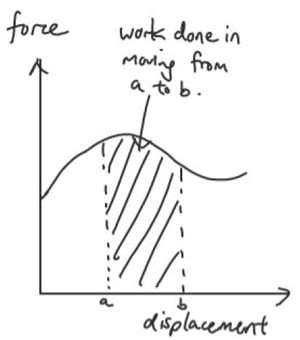
[spoiler title=”Gravitational Field” open=”yes”]

• Newton’s Law of Gravitation states that the gravitational force between two point masses is directly proportional to the product of their masses and inversely proportional to the square of their separation,
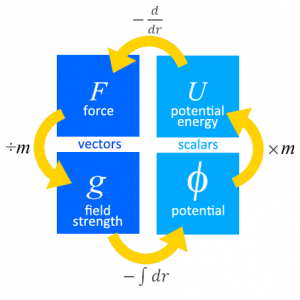
  i.e. $$F_G=\dfrac{Gm_1m_2}{r^2}$$ where G is the gravitational constant 6.67 $$\times$$ 10^-11 N kg^-2m², m₁ and m₂ are the masses and r is the distance between them.
• Gravitational field strength at a point is defined as the gravitational force acting per unit mass placed at that point,
  i.e. $$g=\dfrac{F_G}{m_2}=\dfrac{Gm_1}{r^2}$$ where m₁ is the mass of the source of the field.
• Gravitational potential energy at a point is defined as the work done by an external agent in bringing a body from infinity to that point (without any change in kinetic energy),
  i.e. $$U=-\dfrac{Gm_1m_2}{r}$$
• Gravitational potential at a point is defined as the work done per unit mass by an external agent in bringing a body from infinity to that point (without any change in kinetic energy),
  i.e. $$V=-\dfrac{Gm_1}{r}$$

[/spoiler]

[spoiler title=”Interplanetary Travel”]

• Escape speed is the minimum speed at which a body of mass m can be projected from the surface of a planet of mass M so that it reaches an infinite distance from the planet.
• By conservation of energy,
  initial total energy = final total energy
  $$U_i+E_{k_i}=U_f+E_{k_f}\\-\dfrac{GMm}{r}+\dfrac{1}{2}mv^2=0+0$$
  $$v=\sqrt{2GM}$$

[/spoiler]

[spoiler title=”Satellite Motion”]

• For an object with mass m in orbit,
  Gravitational Force = Centripetal Force
  $$F_G=F_C\\\dfrac{GMm}{r^2}=mr\omega^2\\\dfrac{GM}{r^2}=r(\dfrac{2\pi}{T})^2\\\text{period, }T=2\pi\sqrt{\dfrac{r^3}{GM}}$$
• $$F_G=F_C\\\dfrac{GMm}{r^2}=\dfrac{mv^2}{r}\\\text{orbital speed, }v=\sqrt{\dfrac{GM}{r}}$$
• kinetic energy, $$E_k=\dfrac{1}{2}mv^2=\dfrac{GMm}{2r}$$
• total energy, $$E_T=E_k+U=\dfrac{GMm}{2r}-\dfrac{GMm}{r}=-\dfrac{GMm}{2r}$$

[/spoiler]

[spoiler title=”Geostationary Satellites”]

• A geostationary satellite (one that is always above the same point on the Earth) has to be in an equatorial orbit, i.e. the orbit is in the same plane as that of the equator, so that
  • the centripetal force points towards the centre of the plane, and
  • it moves in the same direction of rotation as the Earth, i.e. from west to east.
• It has a period of 24 h, i.e. same period as the Earth.
• It orbits with a fixed radius of 4.20 $$\times$$ 10⁷ m from the Earth’s centre.

[/spoiler]

[accordions autoHeight=’true’]

[accordion title=”1. Work Done”]

• Work done W is defined as the product of the force and the displacement made in the direction of the force.
  • For a constant force F acting in same direction as the displacement s: W = F . s
  • If $$\theta$$ is the angle between F and s:  $$W = F\cos\theta\cdot s$$

• Work done = Area under F-s graph.

 
[/accordion]

[accordion title=”1.1 Work Done on a Spring”]

• Work done in stretching a spring = area under F-x graph = ½ Fx = ½ kx²

 
[/accordion]

[accordion title=”1.2 Work Done by a Gas”]

• Work done by expanding gas = area under P-V graph = $$\int P.dV$$

[/accordion]

[accordion title=”2. Kinetic Energy”]

• Kinetic energy is the energy of a body by virtue of its motion.
• Derive kinetic energy: W = F.s = ma.s = m ½(v² – u²)

[/accordion]
[accordion title=”3. Potential Energy”]

• Potential energy is the energy of a body by virtue of it position.
• Gravitational Potential Energy near Earth’s surface: $$E_p = mgh$$

[/accordion]

[accordion title=”4. Conservation of Energy”]

• The Principle of Conservation of Energy states that energy can neither be created nor destroyed in any process. It can be transformed from one form to another, and transferred from one body to another but the total amount remains constant.
• The Work-Energy Theorem states that the net work done by external forces acting on a particle is equal to the change in mechanical energy of the particle. i.e. $$W=\Delta E_k+\Delta E_p$$
• Force $$F =-\dfrac{dU}{dx} = -\text{(gradient of Potential Energy vs displacement graph)}$$

[/accordion]

[accordion title=”5. Power”]

• Power is work done per unit time
• Instantaneous Power: $$P = \dfrac{dW}{dt} = F \dfrac{ds}{dt} = F v$$,
• Average Power: $$<P> = \dfrac{W}{t} = F <v>$$

[/accordion]

[accordion title=”6. Efficiency”]

• Efficiency $$\eta= \dfrac{E_{output}}{E_{input}}\times 100 \% \text{ or} \dfrac{P_{output}}{P_{input}}\times100\%$$

[/accordion]
[/accordions]