Seng Kwang Tan

25 December

Measuring Speed of Sound

Seng Kwang Tan 12 Superposition, Demonstrations, IP3 08 General Wave Properties (Sound) 0 Comments

Outline for Measuring the Speed of Sound Using a Tuning Fork and a Hollow Pipe Submerged in Water:

  1. Equipment Setup:
    • Obtain a tuning fork of known frequency and a hollow pipe that can be partially submerged in a column of water.
    • The pipe should be open at the top and closed at the bottom by the water surface.
  2. Strike the Tuning Fork:
    • Strike the tuning fork on a soft surface to make it vibrate. This produces a sound wave of a specific frequency, known as the fundamental frequency of the tuning fork.
  3. Submerge the Hollow Pipe:
    • Submerge the hollow pipe vertically in a large container filled with water. The length of the air column inside the pipe can be adjusted by raising or lowering the pipe in the water.
  4. Create Resonance:
    • Hold the vibrating tuning fork above the open end of the pipe. Slowly raise or lower the pipe in the water while listening for the loudest sound, which indicates resonance.
    • Resonance occurs when the length of the air column in the pipe is such that it forms a standing wave with the frequency of the tuning fork. This usually happens when the length of the air column is a quarter of the wavelength of the sound wave.
  5. Measure the Air Column Length:
    • When resonance is achieved (indicated by a significant increase in sound amplitude), measure the length of the air column from the water surface to the top of the pipe. This length corresponds to one-quarter of the wavelength of the sound wave in air.
  6. Calculate the Wavelength:
    • Multiply the measured length by 4 to determine the wavelength of the sound wave.
  7. Determine the Speed of Sound:
    • Use the formula Speed of Sound = Frequency × Wavelength ($v = f\lambda$) to calculate the speed of sound in air. The frequency is given by the tuning fork, and the wavelength is obtained from the previous step.

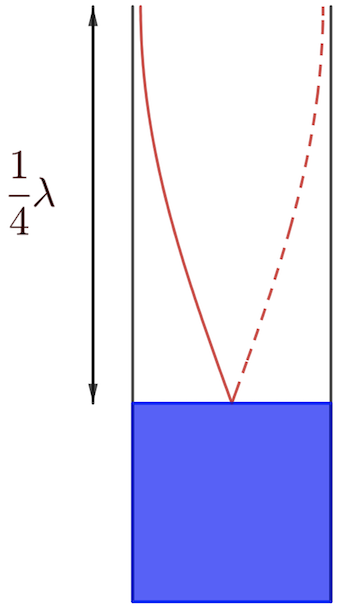
Explanation:

The speed of sound in air can be measured using the relationship between the frequency of the sound wave and its wavelength, which are connected by the speed of sound. When the tuning fork vibrates, it creates sound waves that travel through the air. When these waves enter the hollow pipe, they reflect off the water surface, and at certain lengths, they create a resonance condition, amplifying the sound. The resonant length corresponds to one-quarter of the wavelength because the pipe is effectively closed at the bottom (by the water), forming a node at the water surface and an antinode at the open end. By measuring this length and knowing the frequency of the tuning fork, the speed of sound can be calculated.

25 December

Hanging Forks

Seng Kwang Tan 04 Forces, Demonstrations, IP3 04 Forces 0 Comments

This simple demonstration can be done anywhere at home using the following items:

  1. an empty glass
  2. a toothpick
  3. two forks
The video below demonstrates how to do it. When the forks are balanced on the mouth of the glass with the toothpick, the centre of gravity of the forks-and-toothpick system will adjust itself so that it lies vertically below the pivoting point. This is possible because the forks form a V-shape within which the centre of gravity can exist.

25 December

Cartesian Diver

Seng Kwang Tan 04 Forces, Demonstrations, IP3 05 Density and Pressure 1 Comment

Ever wondered how a submarine sinks and floats? The demonstration here can be used to explain the changes in forces involved and is going to impress most people who see it for the first time. It consists of a floating object inside a sealed plastic bottle that sinks when the bottle is given a tight squeeze and floats again when the squeeze is released.

I have seen the Cartesian diver being made with something else, such as a packet of ketchup or a dropper. The method given below works better than those and uses things that are easily available around the house.

Materials

  1. A plastic water-bottle
  2. A pen cap
  3. Some modelling clay
  4. Water

Procedure

  1. The first step is to attach some modelling clay on the tail of the pen cap to serve as weight so that when placed into water, the pen cap floats upright. There has to be just enough weight added so that the pen cap will “just float”. That is, if any more is added, the cap will sink. It takes some time to find the balance and the best way to do so is to test it in a basin of water.
  2. Once the correct weight is attached to the pen cap, place it upright into the filled water bottle and close the cap.
  3. Test it out by giving the bottle a tight squeeze. (If it remains afloat even when you have given it the tightest squeeze, take the pen cap out and add more weight.
  4. If it sinks straightaway, remove some weight. This should not be necessary if we have already carried ou the t test in the basin.)

Physics Principles Explained

There are two ways to explain this demonstration, one for those who cannot be bothered with equations, and the other for those who are keen on delving deeper.

Using the simple idea of density, we can explain that when the bottle is squeezed, some of the water enters the pen cap and compresses the air trapped within. Hence, the collective density of the submerged pen cap, together with its air and water content, increases. (Note that we are not referring to the density of the pen cap alone, which is a constant.) When this density exceeds that of the water around it, the pen cap sinks. The action is reversed when the squeeze is released.

Some would prefer an alternative explanation. This invokes the idea of forces acting on the pen cap, namely, upthrust and weight. Archimedes’ principle, otherwise known as the law of buoyancy, states that the any object that is partially or fully submerged in a fluid (liquid or gas) experiences an upward force known as the upthrust that is equal in magnitude to the weight of the fluid which is displaced. In mathematical terms,

$$U=\rho Vg$$

where $\rho$ is the density of the fluid, V is the volume of the fluid that is displaced and g is the acceleration of free-fall.

This force opposes the weight of the object and the result determines the direction that the object will move.

For the case of the Carteesian diver, upthrust is varied by changing the volume of fluid, V, that is displaced by the air within the pen cap. When the bottle is squeezed, part of the original volume of air is now occupied by the water which enters due to a higher pressure. This means that the volume of fluid displaced decreases, and as a result, upthrust decreases.

Free-Body Diagram