Subject Content

• The root-mean-square value of an alternating current is equivalent to the steady direct current that would dissipate heat at the same rate as the alternating current in a given resistor.
• For a sinusoidal source,
  (a) the root mean square value of the current is given by 𝐼𝑟⁢𝑚⁢𝑠=𝐼𝑜√2.
  (b) the mean or average power < P > absorbed by a resistive load is half the maximum power.
  <𝑃>=12⁢𝑃𝑜=12⁢𝐼𝑜⁢𝑉𝑜=12⁢𝐼𝑜2⁢𝑅=𝑉2𝑜2⁢𝑅.
  
• An a.c. transformer is a device for increasing or decreasing an a.c. voltage. It consists of a primary coil of N_p turns and voltage V_p and secondary coil of N_s turns and voltage V_s wrapped around an iron core.
• For an ideal transformer (assuming no energy is lost), the following equation is obeyed
  𝑁𝑠𝑁𝑝=𝑉𝑠𝑉𝑝=𝐼𝑝𝐼𝑠.
• Power loss in the transmission lines is minimized if the power is transmitted at high voltages (i.e. low currents) since 𝑃𝑙⁢𝑜⁢𝑠⁢𝑠=𝐼2⁢𝑅 where I is the current through the cables and R is the resistance of the cables.
• The equation 𝑃=𝑉2𝑅 is often mistakenly used to suggest that power lost is high when voltage of transmission is high. In fact, V refers to the potential difference across the cables, which often have but a fraction of the overall resistance through which the current passes.

[accordions autoHeight=’true’]

[accordion title=”1. Particle Nature of Light”]

• A photon is a quantum of electromagnetic radiation.
• The energy of a photon is given by E=hf, where h is Planck’s constant (6.63 × 10^-34 J s) and f is its frequency.

[/accordion]

[accordion title=”1.1 Photoelectric Effect”]

• The photoelectric effect is the emission of electrons from a metal surface when electromagnetic radiation of sufficiently high frequency is shone on it.
• The energy of an incident photon is the sum of the maximum kinetic energy 𝐾.𝐸.𝑚𝑎𝑥 of the emitted electrons from the metal surface and the work function Φ of the metal. Einstein’s photoelectric equation states that

ℎ⁡𝑓=Φ+𝐾.𝐸.𝑚𝑎𝑥=ℎ⁡𝑓𝑜+𝐾.𝐸.𝑚𝑎𝑥

• where 𝑓𝑜 is the threshold frequency or minimum frequency of the electromagnetic radiation below which no electrons are emitted from the metal surface regardless of the intensity of the radiation.
• The work function Φ of a metal is the minimum energy needed to remove an electron from the metal surface.
• 𝐾.𝐸.𝑚𝑎𝑥 can be measured by applying a voltage to prevent the emitted electrons from reaching the electrode that collects them. This voltage is known as the stopping voltage 𝑉𝑠 and since the charge of an electron is e, the equation can be rewritten as

ℎ⁡𝑓=Φ+𝑒⁢𝑉𝑠.

[/accordion]

[accordion title=”1.2 Line Spectra”]

• An atom is in the ground state when its electron occupies the lowest energy level. When the atom gains energy, its ground state electron makes a transition to a higher energy level. The atom is said to be in an excited state.
• At this excited state, the electron is unstable. It will jump to a lower energy level by emitting a photon whose energy is equal to the energy difference between the two levels. The photon energy is given hf = E_higher – E_lower.
• The emission line spectra are the spectra of light radiated by individual atoms in a hot gas when the electrons in the atoms jump from higher energy levels to lower energy levels. Each spectrum consists of coloured lines on a dark background.
• The absorption line spectra consists of dark lines on a coloured background. When a beam of white light is passed through a cool gas, photons whose energies are equal to the excitation energies of the gas atoms, are absorbed. These photons are re-emitted in all directions, so the intensity of these wavelengths in the transmitted white light beam is reduced.

[/accordion]

[accordion title=”2. Wave Nature of Particles”]

• Louis de Broglie postulated that, because photons have wave and particle characteristics, perhaps all forms of matter have both properties. Electron diffraction provides evidence for the wave nature of particles.
• The de Broglie wavelength of a particle is given by 𝜆=ℎ𝑝 where p is the momentum (mv) of the particle and h is Planck’s constant.

[/accordion]

[accordion title=”3. X-ray Spectrum”]

[/accordion]

[accordion title=”4. Heisenberg Uncertainty Principle”]

[/accordion]

[accordion title=”5. Wave Function and Probability”]

• An electron can be described by a wave function Ψ where the square of the amplitude of the wave function |Ψ|2 gives the probability of finding the electron at a point.

[/accordion]

[accordion title=”6. Quantum Tunneling”]

• Classically, an electron of energy E approaching a potential barrier, whose height U is greater than E, cannot penetrate the barrier but would simply be reflected and return in the opposite direction.
• However, quantum mechanics predicts that since |Ψ2| is non-zero beyond the barrier, there is a finite chance of this electron tunnelling through the barrier and reaching the other side of the barrier.
• The transmission coefficient T represents the probability with which an approaching electron will penetrate to the other side of the barrier. The transmission coefficient T is given by 𝑇=𝑒−2⁢𝑘⁢𝑑 where 𝑘=√8⁢𝜋2⁢𝑚⁢(𝑈−𝐸)ℎ2

[/accordion]

[/accordions]

The Nucleus

• existence and size demonstrated using the Rutherford 𝛼-scattering experiment.
• consists of nucleons (protons and neutrons)
• isotopes of an element share the same number of protons but different number of neutrons.

Nuclear Reactions

• nuclear reactions involve two or more reactants.
• represented using the form: 147⁢𝑁+42⁢𝐻⁡𝑒→178⁢𝑂+11⁢𝐻
• for a reaction that releases energy, mass-energy of reactants = mass-energy of products + E,
  where 𝐸=𝑚⁢𝑐2 and m is the mass defect (difference in mass between the products and reactants).
• binding energy is the energy released when the nucleus is formed from its separate protons and neutrons. The same amount of energy is required to break up a nucleus into its constituent nucleons.

• binding energy per nucleon (𝐵.𝐸.𝐴) is an indication of the stability of a nucleus, where B.E .is binding energy and A is the nucleon number. You need to know how to sketch its variation with nucleon number. (The following video explains the shape of the 𝐵.𝐸.𝐴 versus A graph and why it peaks at 56⁢𝐹⁡𝑒.

• nuclear fission is the disintegration of a heavy nucleus into two lighter nuclei of comparable mass with the emission of neutrons and release of energy.
  e.g. 23592⁢𝑈+10⁢𝑛→23692⁢𝑈→14456⁢𝐵⁢𝑎+9036⁢𝐾⁢𝑟+210⁢𝑛+𝐸⁢𝑛⁢𝑒⁢𝑟⁢𝑔⁡𝑦
• nuclear fusion occurs when two light nuclei combine to form a single more massive nucleus, leading to the release of energy.
  e.g. 21⁢𝐻+31⁢𝐻→42⁢𝐻⁡𝑒+10⁢𝑛+𝐸⁢𝑛⁢𝑒⁢𝑟⁢𝑔⁡𝑦

• The following quantities are always conserved:
  • proton number & neutron number
  • momentum
  • mass-energy

Radioactive Decay

• spontaneous and random emission of radiation from a radioactive nucleus.
  • 𝛼 particle – helium nucleus
  • 𝛽 particle – electron
  • 𝛾 particle – electromagnetic radiation

http://youtu.be/Qlb5Z8QBpcI

• 𝐴=−𝑑⁢𝑁𝑑⁢𝑡=𝜆⁢𝑁
  where A is the rate of disintegration or activity, N is the number of radioactive nuclei and 𝜆 is the decay constant.
• 𝑥=𝑥0⁢𝑒−𝜆⁢𝑡
  where x could represent the activity, number of undecayed particles or received count rate.
• half-life (𝑡12) is the average time taken for half the original number of radioactive nuclei to decay.
• From 𝑥=𝑥0⁢𝑒−𝜆⁢𝑡,
  𝑥𝑥0=12=𝑒−𝜆⁢𝑡12
  ⇒−𝑙⁢𝑛⁢2=−𝜆⁢𝑡12
  ⇒𝑡12=𝑙⁢𝑛⁢2𝜆
• You may also use 𝑥𝑥0=12𝑡𝑡1/2, as shown in the following video.

[accordions autoHeight=’true’]

[accordion title=”1. Definitions”]

• The magnetic flux density at a point is defined as the force acting per unit current per unit length of the conductor when the conductor is placed at right angles to the field.
• One tesla is the uniform magnetic flux density which, acting normally to a long straight wire carrying a current of 1 ampere, causes a force per unit length of 1 N m^–1 on the conductor.

[/accordion]

[accordion title=”2. Magnetic Fields”]

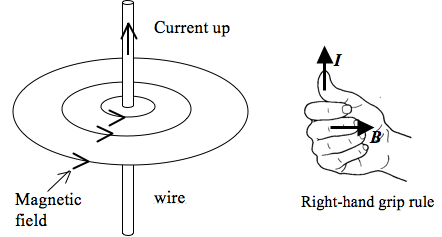
• The following are the vector symbols used in diagrams to represent the direction of vectors in 3 dimensional space:
  • → : on the plane of the page
  • ⊗ : into of the page
  • ⊙ : out of the page
• The following are some important points to take note when representing a magnetic field by magnetic field lines:
  • Magnetic field lines appear to originate from the north pole and end on the south pole.
  • Magnetic field lines are smooth curves.
  • Magnetic field lines never touch or cross.
  • The strength of the magnetic field is indicated by the distance between the lines – closer lines mean a stronger field.

[/accordion]

[accordion title=”3. Force on a Current-Carrying Conductor in a Magnetic Field”]

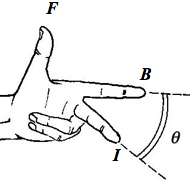
• When a wire of length 𝑙 carrying a current 𝐼 lies in a magnetic field of flux density 𝐵 and the angle between the current 𝐼 and the field lines 𝐵 is 𝜃, the magnitude of the force 𝐹 on the conductor is given by 𝐹=𝐵⁢𝐼⁢𝑙⁢𝑠⁢𝑖⁢𝑛⁢𝜃.
  
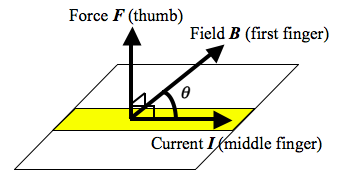
• The directions of the vectors can be recalled by using the Fleming’s Left-Hand Rule.
  

[/accordion]

[accordion title=”4. Force on a Moving Charge in a Magnetic Field”]

• A charge 𝑞 travelling at constant speed 𝑣 at an angle 𝑡⁢ℎ⁡𝑒⁢𝑡⁢𝑎 to a magnetic field of flux density 𝐵 experiences a force 𝐹=𝐵⁢𝑞⁢𝑣⁢𝑠⁢𝑖⁢𝑛⁢𝜃.

[/accordion]

[accordion title=”5. Magnetic fields of current-carrying conductors”]

• Long straight wire
  
• Flat circular coil
• Solenoid

[/accordion]

[accordion title=”6. Ferromagnetic Materials”]

[/accordion]

[accordion title=”7. Force between Two Parallel Current-Carrying Conductors”]

•  Like currents attract and unlike currents repel.

[/accordion]

[/accordions]