Demonstrations

Physics demonstrations for all.

07 February

Exploring Motion with a Ticker Tape Timer

Seng Kwang Tan Demonstrations, IP3 02 Kinematics 0 Comments

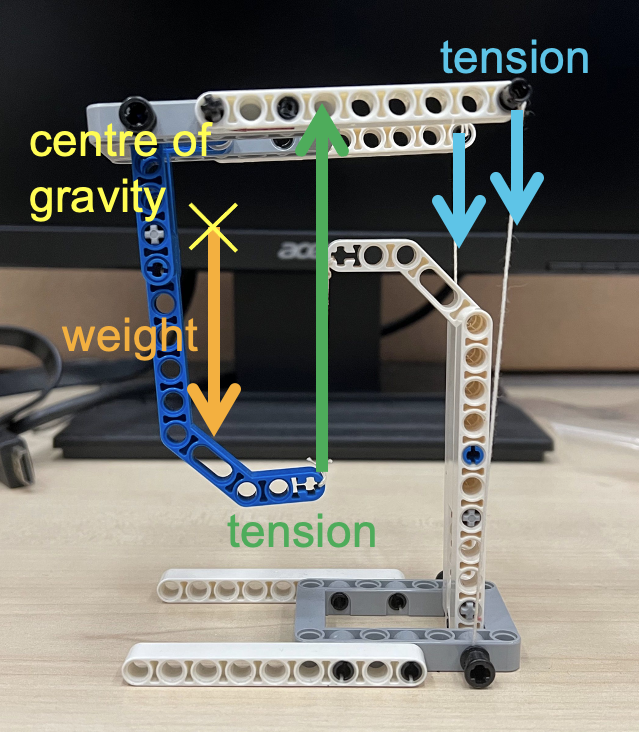
This week, I conducted a lesson on motion for my IP3 class using a simple yet effective tool: a simulated ticker tape timer. The objective was to help students develop an intuitive understanding of uniform and non-uniform motion by actively engaging in an experiment.

Introduction to the Ticker Tape Timer

To kickstart the lesson, I showed my students a YouTube video that explains how a ticker tape timer works:

This video provided a visual demonstration of how a ticker tape timer marks regular intervals on a moving strip of paper, allowing us to analyze motion quantitatively.

Hands-On Experiment: Simulating a Ticker Tape Timer

After the video, I had students pair up for a hands-on activity. Instead of using an actual ticker tape timer, we simulated the process using paper strips cut from A3-sized sheets. Each pair had one student act as the “moving arm,” responsible for placing dots on the strip, while the other played the role of the “puller,” responsible for pulling the paper strip at different speeds.

To ensure a consistent time interval between each dot, I used a Metronome App that I created:

This app produces a steady rhythm at 120 beats per minute, meaning that the interval between each beep (and consequently each dot) is 0.5 seconds. To improve accuracy, the student acting as the moving arm was instructed to close their eyes and focus solely on the beep.

Step 1: Recording Uniform Motion

In the first trial, the puller was asked to pull the paper at a constant rate. As the paper moved steadily, the moving arm marked dots at regular intervals based on the metronome beat. After completing the trial, students used a ruler to measure the distances between successive dots. Since the time interval was fixed, they could easily calculate the speed of the paper by using:

Step 2: Recording Accelerated Motion

Next, the students switched roles. This time, the new puller was asked to gradually increase the speed of the paper. As expected, the spacing between dots increased progressively, providing a clear visual representation of acceleration. This led to discussions on how motion can be analyzed using dot patterns and how acceleration differs from uniform motion.

Reflections and Key Takeaways

This activity was highly effective in reinforcing key motion concepts. Since we do not have an actual ticker tape machine, it allowed students to engage in a hands-on simulation while visually and physically experience motion rather than just reading about it.

Next Steps

To extend this lesson, I plan to introduce velocity-time graphs and have students plot their measured speeds to analyze changes in motion further. Additionally, incorporating digital tools like video analysis with Tracker software could help reinforce these concepts further.

If you have any feedback or suggestions, feel free to share them in the comments below!

28 April

Tensegrity Explained

Seng Kwang Tan 04 Forces, Demonstrations, IP3 04 Forces, Lego 1 Comment

There is a new internet trend called “tensegrity” – an amalgamation of the words tension and integrity. It is basically a trend of videos showing how objects appear to float above a structure while experiencing tensions that appear to pull parts of the floating object downwards.

In the diagram below, the red vectors show the tensions acting on the “floating” object while the green vector shows the weight of the object.

The main force that makes this possible is the upward tension (shown below) exerted by the string from which the lowest point of the object is suspended. The other tensions are downward and serve to balance the moment created by the weight of the object. The centre of gravity of the “floating” structure lies just in front of the supporting string. The two smaller downward vectors at the back due to the strings balance the moment due to the weight, and give the structure stability sideways.

This is a fun demonstration to teach the principle of moments, and concepts of equilibrium.

The next image labels the forces acting on the upper structure. Notice that the centre of gravity lies somewhere in empty space due to its shape.

Only the forces acting on the upper half of the structure are drawn in this image to illustrate why it is able to remain in equilibrium

These tensegrity structures are very easy to build if you understand the physics behind them. Some tips on building such structures:

  1. Make the two strings exerting the downward tensions are easy to adjust by using technic pins to stick them into bricks with holes. You can simply pull to release more string in order to achieve the right balance.
  2. The two strings should be sufficiently far apart to prevent the floating structure from tilting too easily to the side.
  3. The centre of gravity of the floating structure must be in front of the string exerting the upward tension.
  4. The base must be wide enough to provide some stability so that the whole structure does not topple.

Here’s another tensegrity structure that I built: this time, with a Lego construction theme.

Apart from using Lego, I have also 3D-printed a tensegrity structure that only requires rubber bands to hold up. In this case, the centre of gravity of the upper structure is somewhere more central with respect to the base structure. Hence, 3 rubber bands of almost equal tension will be used to provide the balance. The STL file for the 3D model can be downloaded from Thingiverse.com.

The main challenge in assembling a tensegrity structure is the adjustment of the tensions such that the upper structure is balanced. One way to simplify that, for beginners, is to use one that is supported by rubber bands as the rubber bands can adjust their lengths according to the tensions required.

3D-printed tensegrity table balanced by rubber bands

Another tip is to use some blu-tack instead of tying the knots dead such as in the photo below. This is a 3D printed structure, also from Thingiverse.

3D-printed tensegrity table held up and balanced by nylon string

(This post was first published on 18 April 2020 and is revised on 24 August 2022.)

16 July

Braking of a Magnetic Pendulum with Copper Plate

Seng Kwang Tan 18 Electromagnetic Induction, Demonstrations 0 Comments

In this video, we will observe how induced eddy currents in a copper plate slow down a magnetic pendulum. 

When the pendulum is set in motion, it usually oscillates for quite a while. This pendulum consists of a strong magnet.

If we slide a copper plate underneath the magnet while it is in motion, the magnet comes to a stop quickly. Note that copper is not a ferromagnetic material, which means it does not get attracted to a stationary magnet.

As the magnet moves across an area on the copper plate, the change in magnetic flux induces eddy currents on the plate. These eddy currents flow in such a way as to repel the magnet as it approaches the plate and attracts the magnet as it leaves the plate, therefore slowing the magnetic pendulum.

Eddy currents repels the magnet as it approaches
Eddy currents attracts the magnet as it leaves

When we pull the copper sheet out from under a stationary magnetic pendulum, the eddy currents will flow in such a way that it becomes attracted to the copper sheet.

Moving the copper sheet to and fro at a certain frequency (the pendulum’s natural frequency), the magnetic pendulum can be made to oscillate again.

16 July

Non-Uniform Vertical Circular Motion

Seng Kwang Tan 06 Motion in a Circle, Demonstrations, GeoGebra 0 Comments

Using a chain of rubber bands, I swung a ball around in a vertical loop. This demonstration shows how the tension in an elastic band changes according to the position of the ball, by referring to the length of the elastic band.

Securing the elastic band to the ball with a shoelace

When the ball of mass $m$ is at the bottom of the loop, the centripetal force is given by the difference between tension $T_{bottom}$ and weight $mg$, where $T_{bottom}$ varies depending on the speed of the ball $v_{bottom}$ and the radius of the curvature $r_{bottom}$.

$T_{bottom} – mg = \dfrac{mv_{bottom}^2}{r_{bottom}}$

When the ball is at the top of the path, it is given by

$T_{top} + mg = \dfrac{mv_{top}^2}{r_{top}}$

As the weight is acting in the same direction to tension when the ball is at the top, a smaller tension is exerted by the elastic band to maintain a centripetal force. Therefore , $T_{bottom} > T_{top}$.

The GeoGebra app below shows a simpler version of a vertical loop – a circular path with a fixed radius $r$. Consider a ball sliding around a smooth circular loop. The normal contact force varies such that

$N_{bottom} = \dfrac{mv_{bottom}^2}{r} + mg$

$N_{top} = \dfrac{mv_{top}^2}{r} – mg$

It can be shown that the minimum height at which the ball must be released in order for it to complete the loop without losing contact with the track is 2.5 times the radius of the frictionless circular track.

If we were to consider the rotational kinetic energy required for the ball to roll, the required initial height will have to be 2.7 times the radius, as shown in the video below:

Many thanks to Dr Darren Tan for his input. Do check out his EJSS simulation of a mass-spring motion in a vertical plane, which comes with many more features such as the ability to vary the initial velocity of the mass, graphs showing the variation of energy and velocity, as well as an option for a mass-string motion as well.

29 March

Measuring speed of sound in air using Audacity

Seng Kwang Tan 11 Wave Motion, Demonstrations, IP3 08 General Wave Properties (Sound) 0 Comments

A physics demonstration on how to measure the speed of sound in air using Audacity, an open source audio recording software. There are Windows and Mac versions of this free software, and even a portable version that can run off a flash drive without needing to be installed on a computer (for school systems with stricter measures regarding installing of software).

The sound is reflected along a long hollow tube that somehow, existed in our school’s laboratory. The two sound signals were picked up using a clip-on microphone attached to the open end of the tube and plugged into the laptop. I used my son’s castanet which gives a crisp sound and hence, a simple waveform that will not have the echo overlapping with the generated sound. The timing at which the sound signals were first detected were read and subtracted to obtain the time taken for the wave to travel up and down the 237 cm tube.

The value of the speed of sound calculated is 356 m/s, which is a bit on the high side due to the temperature of 35°C and relative humidity of between 60-95% when the reading was carried out.

If you are interested, you can check out how the software can be used to determine the frequency of a tuning fork.