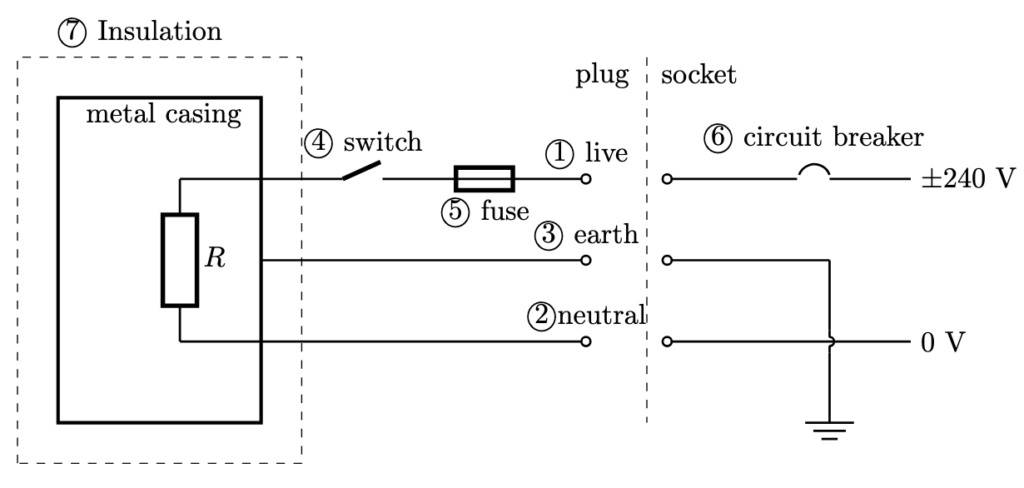
- Live wire: wire carrying the current at a high voltage from the power source to the electrical appliance.
- Neutral wire: wire completing the circuit by carrying current back to the power source, maintaining a low potential close to zero volts.
- Earth wire: wire provides a path for electrical current to flow safely into the ground in case of a fault, preventing the appliance’s exterior from becoming live and reducing the risk of electric shock.
- Switch: a device that opens and closes the circuit. Connected to the live wire instead of neutral wire so that device does not remain live when current is off.
- Fuse: a safety device connected to the live wire and is designed to melt/break, thus creating an open circuit, when the current passing through it exceeds a specified value. Its current rating should just be slightly higher than the normal operating current.
- Circuit breaker: a safety device connected to the live wire which switches off the electrical supply when a excessive current flows through it.
- Double insulation: two layers of protection to prevent users from coming into contact with live electrical parts, eliminating the need for an earth connection.
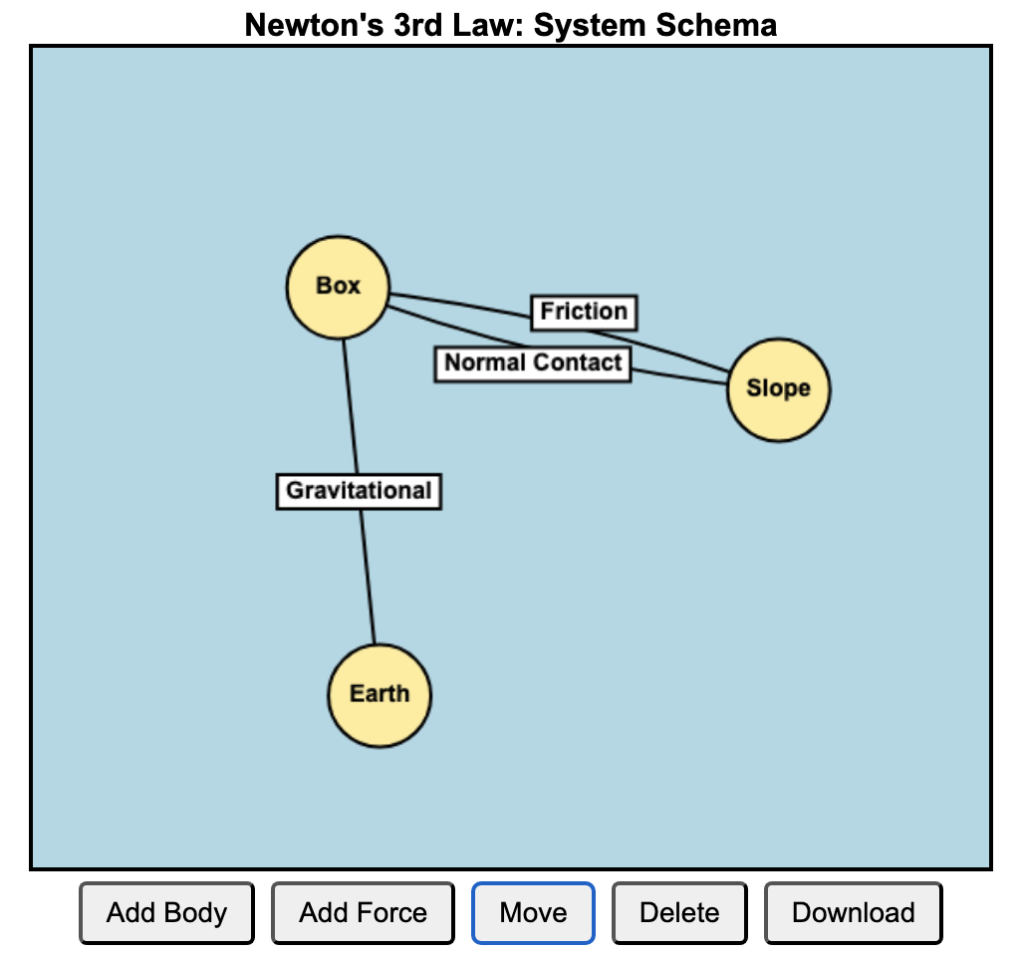
Example Scenarios
Fault: You accidentally run over the iron’s cord with a chair, exposing the internal wires. Exposed live wire touches the metal casing.
Protection:
- Earth Wire diverts the fault current safely to the ground.
- Circuit Breaker detects the sudden surge and cuts off power immediately OR
- Fuse in the plug blows to break the circuit.
- If the appliance had Double Insulation, the user will not be able to touch the metal casing.
Fault: You plug too many devices into the same extension cord, leading to overloading — the total current drawn exceeds the safe current rating.
Protection:
- Fuse in the plug blows to break the circuit.
- Circuit Breaker in the consumer unit (distribution board) trips, cutting off power.