11 Wave Motion

26 August

Phase Difference

Seng Kwang Tan 11 Wave Motion, GeoGebra 4 Comments

The first of two apps on Phase Difference allows for interaction to demonstrate the oscillation of two different particles along the same wave with a variable phase difference.

The second shows two waves also with a phase difference.

In both cases, the phase difference $\Delta\phi$ can be calculated with

$$\Delta\phi = \dfrac{\Delta x}{\lambda} \times 2\pi$$

where $\Delta x$ is the horizontal distance between the two particles or the horizontal distance between the two adjacent identical particles (one from each wave) and $\lambda$ is the wavelength of the waves.

25 August

Longitudinal and Transverse Waves

Seng Kwang Tan 11 Wave Motion, GeoGebra, IP3 08 General Wave Properties 0 Comments

I modified Tom Walsh’s original GeoGebra app to add a moveable single oscillating particle for students to observe its movement along a longitudinal wave and a transverse wave.

The app can also be used to show how the displacement of a particle in a longitudinal wave can be mapped onto a sinusoidal function, similar to the shape of a transverse wave. For example. a displacement of the particle to the right can be represented by a positive displacement value on the displacement-distance graph.

You can choose to select the particle that you want to focus on by using the slider.

For a full screen view, visit https://www.geogebra.org/m/auyft2pd

Here is an animated gif for those who prefer to insert it into a powerpoint slideshow instead:

Animation of longitudinal wave and transverse wave

For embedding into SLS or any platform that supports iframes.

<iframe scrolling="no" title="Progressive Waves" src="https://www.geogebra.org/material/iframe/id/auyft2pd/width/640/height/480/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false" width="640px" height="480px" style="border:0px;"> </iframe>

25 August

Movement of Particle in a Wave

Seng Kwang Tan 11 Wave Motion, GeoGebra, IP3 08 General Wave Properties 0 Comments

This GeoGebra app allows students to observe closely the movement of a particle in a progressive wave, with two possible directions of energy propagation.

In a typical question, students will be asked to predict the next movement of a particle given that a wave is moving left or right. Usually, students will need to imagine the waveform shifting slightly to the left or right in order to figure that out. This app follows the same visualisation technique to identify the subsequent movement of any particle along a wave.

02 July

Phase Difference GeoGebra Apps

Seng Kwang Tan 11 Wave Motion, 12 Superposition, GeoGebra 0 Comments

I created a series of GeoGebra apps for the JC topics of Waves and Superposition, mainly on the concept of Phase Difference. The sizes of these GeoGebra apps are optimised for embedding into SLS. When I have time, I will create detailed instructions on how to create such apps. Meanwhile, feel free to use them.

Instructions on how to embed the apps into SLS can be found in the SLS user guide.

Phase difference between two particles on a progressive wave. Move the particles along the wave to see the value.

Phase difference between two particles on a stationary wave. Move the particles along the wave to observe how their velocities are different or similar.

Observe velocity vectors of multiple particles on a progressive wave.

20 August

Wavefront

Seng Kwang Tan 11 Wave Motion, GeoGebra, Simulations 0 Comments

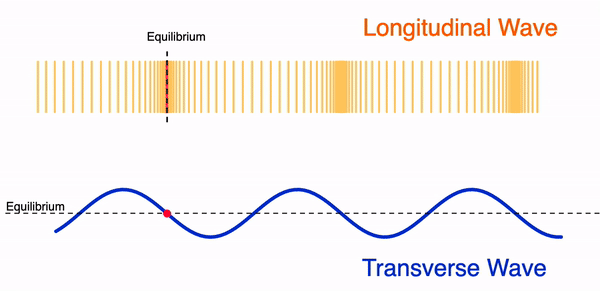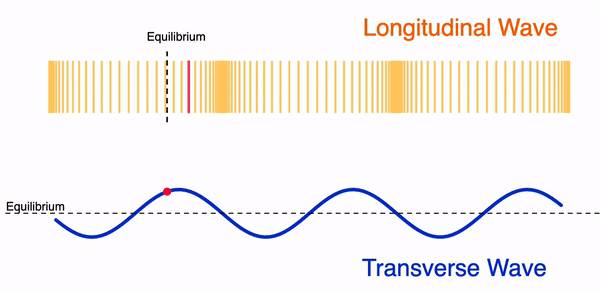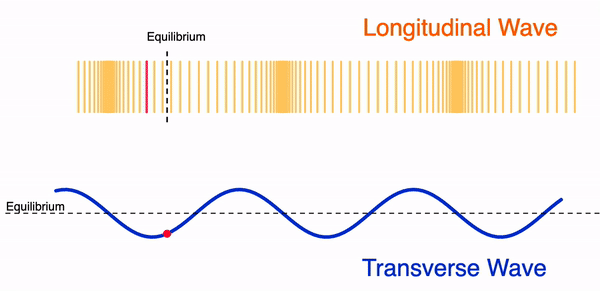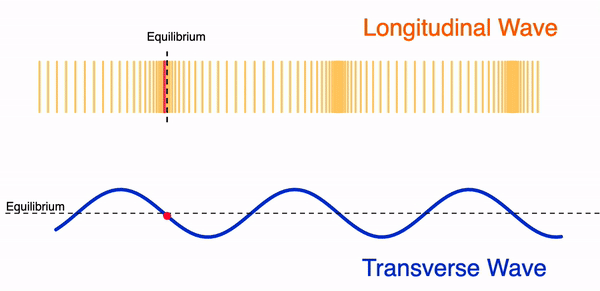
In order to help students visualise a wavefront, a 3-D image is usually used to show the imaginary line joining particles in phase. I created the GeoGebra apps below to allow students to change the wavefront and observe it move with time at a constant wave speed. There represent simplified versions of waves on a ripple tank with a linear and circular wavefront.

Linear Wavefront

A wavefront for a linear wave is a straight line that represents points of equal phase, typically generated by a plane wave source. These wavefronts are parallel to each other and move in a uniform direction as the wave propagates.

GeoGebra link: https://www.geogebra.org/m/rbjcszuc

Rotating the first waveform, you can get the displacement-distance profile of a wave, which is basically the cross-section of a 3-D wave.

Circular Wavefront

A wavefront for a circular wave is a continuous line or curve that represents points of equal phase, emanating outward from a central source. In a two-dimensional medium, these wavefronts are concentric circles that expand as the wave propagates away from the source.

GeoGebra link: https://www.geogebra.org/m/axdhtccg

12 August

Graphs of a Progressive Wave – Geogebra App

Seng Kwang Tan 11 Wave Motion, GeoGebra, Simulations 0 Comments

GeoGebra link: https://www.geogebra.org/m/f7faw3r6

This simple Geogebra app allows students to observe the oscillation of a particle perpendicular to the direction of energy transfer.