A-level Topics

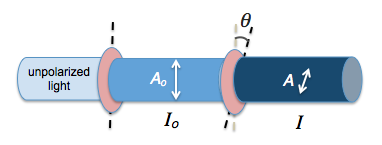
In what seems like a counter-intuitive demonstration, we can place a polarizing filter in between two other filters which do not transmit light in order to cause light to pass through again.

This is because each filter will permit the components of electric field vectors of the electromagnetic waves that are parallel to its axis of polarization according to the equation $$A = A_o \cos{\theta}$$ where $A_o$ is the original amplitude of the unpolarized wave incident on the filter and $\theta$ is the angle between the electric field vector and the axis of polarization. Each time the wave passes through a filter, it undergoes a reduction in amplitude according to the equation so that by the third filter, its resultant amplitude is
$$A = A_o \cos{\theta_1} \cos{\theta_2}$$
where $\theta_i$ is the angle between the axis of polarization of the i^th filter and the electric field vector direction of the incident light on the i^th filter.

According to Malus’ law, the intensity of the light that passes through these two filters is given by

$$I=I_o\cos^2\theta$$

where I₀ is the initial intensity and θ is the angle between the light’s initial polarization direction and the axis of the polarizer.

The resulting intensity for light that passes through 3 filters is given by

$$I=I_o \cos^2{\theta_1}\cos^2{\theta_2}$$

where $\theta_1$ is the angle between the axes of the first and second filters and $theta_2$ is the angle between the axes of the second and third filters.

Using a pair of polarizing sunglasses, you can demonstrate the effects of polarization together with a computer screen which is also polarizing. When the axes of polarization of the two polarizing screens are rotated, the brightness alternates between bright and dark.

Light coming from a computer screen is usually polarized. In the video below, when polarized light passes through another polarizer, the intensity of the light is given by Malus’ law:

$$I = I_o cos ^2{\theta}$$

where $$\theta$$ is the angle between the two axes of polarization and $$I_o$$ is the original intensity of the unpolarized light.

Only the components of electric field vectors in electromagnetic radiation that are parallel to the axis of polarization of a polarizing filter will be permitted through. Those electric field components that are perpendicular to the polarization axis are blocked by the filter.

Hence, the amplitude of a vector A that passes through is given by $$A = A_o \cos{\theta}$$. Since intensity is proportional to the square of amplitude ($$ I \propto {A^2}$$), we have Malus’ law.

The purpose of having polarizing filters in sunglasses and computer screens is to cut out glare due to light from other sources.