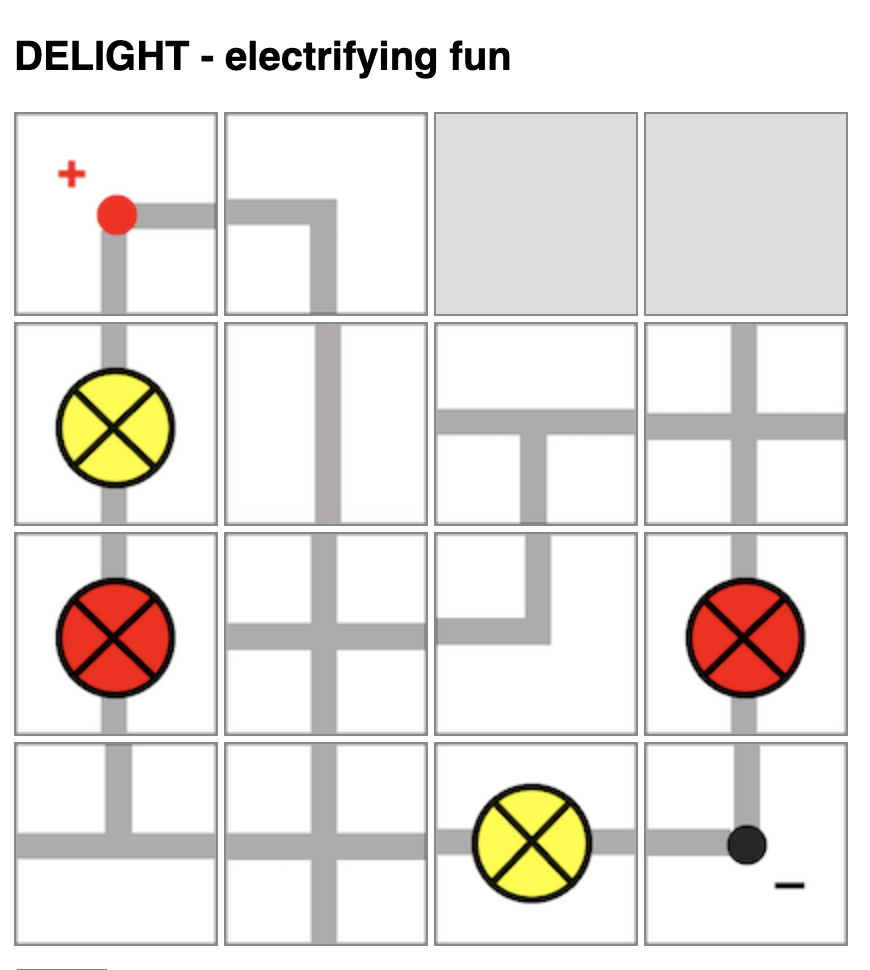
The simulation below allows students to practise calculating potential differences and currents of a slightly complex circuit, involving three different modes that can be toggled by clicking on the switch.
Link: https://www.geogebra.org/m/jkckp9pr
Mode 1: Two Resistors in Series
When resistors \( R_1 \) and \( R_2 \) are connected in series, the total resistance is simply the sum of the individual resistances:
\[ R_{\text{total}} = R_1 + R_2 \]
The current \( I \) through the circuit is given by Ohm’s Law:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} = \frac{V_{\text{total}}}{R_1 + R_2} \]
where \( V_{\text{total}} \) is the total potential difference supplied by the source.
The potential difference across each resistor can be calculated using:
\[ V_1 = I \cdot R_1, \quad V_2 = I \cdot R_2 \]
Mode 2: \( R_1 \) and \( R_3 \) in Parallel, \( R_2 \) in Series
In this mode, resistors \( R_1 \) and \( R_3 \) are in parallel, and \( R_2 \) is in series with the combination. First, calculate the equivalent resistance of the parallel combination:
\[ \frac{1}{R_{\text{parallel}}} = \frac{1}{R_1} + \frac{1}{R_3} \]
Thus, the total resistance is:
\[ R_{\text{total}} = R_{\text{parallel}} + R_2 \]
The current through the circuit is:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} \]
The potential difference across \( R_2 \) is:
\[ V_2 = I \cdot R_2 \]
Since \( R_1 \) and \( R_3 \) are in parallel, they share the same potential difference:
\[ V_1 = V_3 = V_{\text{total}} – V_2 \]
The current through each parallel resistor can be found using Ohm’s Law:
\[ I_1 = \frac{V_1}{R_1}, \quad I_3 = \frac{V_3}{R_3} \]
Mode 3: \( R_1 \) and \( R_2 \) in Series, \( R_3 \) in Parallel
Here, resistors \( R_1 \) and \( R_2 \) are connected in series, and the combination is in parallel with \( R_3 \). First, calculate the resistance of the series combination:
\[ R_{\text{series}} = R_1 + R_2 \]
Then, find the total resistance of the parallel combination:
\[ \frac{1}{R_{\text{total}}} = \frac{1}{R_{\text{series}}} + \frac{1}{R_3} \]
The total current is:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} \]
The voltage across the parallel combination is the same for both branches:
\[ V_1 + V_2 = V_3 = V_{\text{total}} \]
The current through \( R_3 \) is:
\[ I_3 = \frac{V_3}{R_3} \]
The current through \( R_1 \) and \( R_2 \), which are in series, is the same:
\[ I_{\text{series}} = \frac{V_{\text{total}}}{R_1 + R_2} \]
The voltage across each series resistor is:
\[ V_1 = I_{\text{series}} \cdot R_1, \quad V_2 = I_{\text{series}} \cdot R_2 \]
