the world in a different light
For lab work, students often have to estimate a line of best fit for their data points manually. It takes a bit of practice to get it right. With this app, students can generate data points with varying types of scatter and predict their own best-fit line before comparing it with a computer generated one based on the least mean square method.
This simulation can be used for O-level Physics, for the topic of Pressure. I created it as it was relevant to our school’s IP3 physics as well.
It demonstrates the working principle of a hydraulic press. By adjusting the cross-section areas (A) of the two cylinders, you only need a small amount of force at the narrow piston to exert a large amount of force at the wider piston. This is how, when driving, the force applied by one’s foot is enough to supply a large force to apply the brake pads on a car’s wheels.
The advantage of using GeoGebra is that one can create such simple simulations within a couple of hours and it can be readily embedded into Google Classroom, Microsoft OneNote, SLS – a wonderful tool to have during this period of full home-based learning.
While preparing for a bridging class for those JAE JC1s who did not do pure physics in O-levels, I prepared an app on using a vector triangle to “solve problems for a static point mass under the action of 3 forces for 2-dimensional cases”.
For A-level students, they can be encouraged to use either the sine rule or the cosine rule to solve for magnitudes of forces instead of scale drawing, which is often unreliable.
For students who are not familiar with these rules, here is a simple summary:
If you are trying to find the length of a side while knowing only two angles and one side, use sine rule:
$$\dfrac{A}{\sin{a}}=\dfrac{B}{\sin{b}}$$
If you are trying to find the length of a side while knowing only one angle and two sides, use cosine rule:
$$A^2 = B^2 + C^2 – 2BC\cos{a}$$
A ladder rests on rough ground and leans against a rough wall. Its weight W acts through the centre of gravity G. Forces also act on the ladder at P and Q. These forces are P and Q respectively.
Which vector triangle represents the forces on the ladder?
It’s Day 1 of the full home-based learning month in Singapore! As teachers all over Singapore scramble to understand the use of the myriad EdTech tools, I have finally come to settle on a few:
The following is a video that was created using Loom to explain a question on why tension in a rope on which a weight is balanced increases when the rope straightens.
Here are the steps to solving a problem involving Newton’s 2nd law.
Step 1: Draw a free body diagram – where possible, sketch a free body diagram to represent:
Step 2: Write down the equation: $$F_{net}=ma$$
Step 3: Add up the forces on the left-hand side of the equation, making sure that forces acting opposite to the direction of acceleration are subtracted.
Step 4: Solve the equation for the unknown.
For example,
A horizontal force of 12 N is applied to a wooden block of mass 0.60 kg on a rough horizontal surface, and the block accelerates at 4.0 m s-2. What is the magnitude of the frictional force acting on the block?
Step 1: Free-body diagram
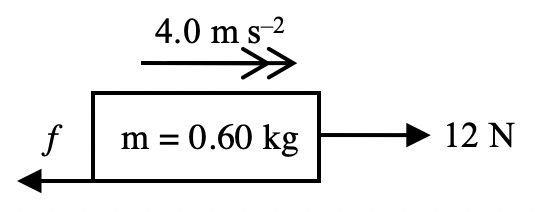
Step 2: Write down the 2nd law equation
By Newton’s 2nd law, $$F_{net}=ma$$
Step 3: Add up the forces making up the net force
$$12 – f = 0.60 (4.0)$$
Step 4: Solve for unknown
$$ f = 12 – 2.4 = 9.6 N$$