This deck of slides are the ones I will be using for the Symposium on “Leveraging Technology for Engaging and Effective Learning” at the Singapore International Science Teachers’ Conference (SISTC) 2024 on Day 2 of the Conference (20 November). Feel free to download for your reference.
In recent years, AI tools like DALL-E and MidJourney have gained popularity for generating stunning, artistic images. However, when it comes to creating scientific illustrations, particularly for exams, we need accuracy, clarity, and precision. This is where LaTeX, a document preparation system widely used in academia, shines. Combined with the intelligence of ChatGPT, LaTeX can produce exactly the images you need without the artistic flair or ambiguity that tools like DALL-E might introduce.
The process of generating science exam images using ChatGPT and LaTeX is straightforward:
- Describe the Diagram: You begin by providing a detailed description of the diagram or scientific illustration you need. For example, “Generate a diagram using Latex showing a free-body diagram of a block on an inclined plane with friction.”
- ChatGPT Generates LaTeX Code: Based on your description, ChatGPT can generate the appropriate LaTeX code, using packages like TikZ or PGFPlots to create the required scientific diagram. The output might look like this:
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
% Inclined plane
\draw[thick] (0,0) -- (4,2);
\draw[thick] (0,0) -- (4,0);
% Block
\draw[fill=gray] (2,1) rectangle (2.5,1.5);
% Forces
\draw[->,thick] (2.25,1.25) -- (2.25,2.25) node[above] {Normal Force};
\draw[->,thick] (2.25,1.25) -- (2.25,0.25) node[below] {Weight};
\draw[->,thick] (2.25,1.25) -- (3.25,1.25) node[right] {Friction};
\end{tikzpicture}
\end{document} - Compile the LaTeX Code: Once the code is generated, you can compile it using any LaTeX editor (such as Overleaf or a local LaTeX distribution).
- Check for Errors: The diagram is unlikely to look perfect in the first iteration. For example, the above code gives the following:

- Edit: You can either instruct ChatGPT to modify specific sections of the diagram or make the changes yourself. After 3 more iterations, for example, ChatGPT produced the following codes:
\begin{tikzpicture}
% Inclined plane
\draw[thick] (0,0) -- (4,2);
\draw[thick] (0,0) -- (4,0);
% Block (rotated to match the slope)
\draw[fill=gray, rotate around={26.565:(2.25,1.25)}] (2,1) rectangle (2.5,1.5);
% Forces (adjusted for friction up the slope)
% Normal Force (perpendicular to the slope)
\draw[->,thick] (2.25,1.25) -- ++(-0.447,0.894) node[above left] {Normal Force};
% Weight (straight down)
\draw[->,thick] (2.25,1.25) -- (2.25,0.25) node[below] {Weight};
% Friction (along the slope, now pointing up the incline)
\draw[->,thick] (2.25,1.25) -- ++(0.894,0.447) node[above right] {Friction};
\end{tikzpicture} - This is the output image:

- Integrate into Teaching Materials: Once you are satisfied with the output, the compiled image can then be saved as a PDF, PNG, or any other image format and directly embedded into your exam materials.
The following are similar images made using the same workflow and their corresponding codes, which I made changes to manually instead as it was faster for me once I became familiar with the coordinate-system based drawing method.
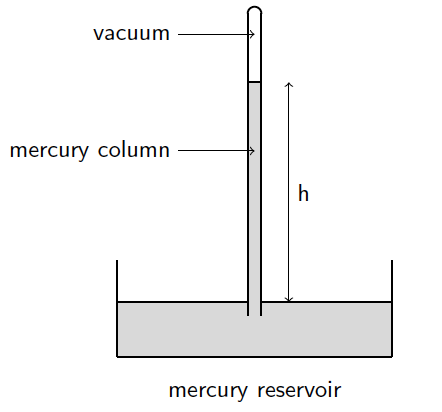
\begin{tikzpicture}
% Draw the base container (mercury reservoir)
\draw[draw=none, fill=gray!30] (-2,-0.2) rectangle (2,-1);
\draw[thick] (-2,-1) -- (-2,0.4);
\draw[thick] (2,-1) -- (2,0.4);
\draw[thick] (-2,-1) -- (2,-1);
\draw[thick] (-2,-0.2) -- (-0.1,-0.2);
\draw[thick] (0.1,-0.2) -- (2,-0.2);
% Mercury inside the tube
\draw[draw=none, fill=gray!30] (-0.1,3) -- (-0.1,-0.3) -- (0.1,-0.3) -- (0.1,3) -- cycle;
\draw[thick] (-0.1,3) -- (0.1,3);
% Draw the glass tube
\draw[thick] (0.1,4) -- (0.1,-0.4); % Tube
\draw[thick] (-0.1,4) -- (-0.1,-0.4); % Tube
% Label for the mercury level
\draw[<-] (0,2) -- (-1.1,2) node[left]{mercury column};
\draw[<-] (0,3.7) -- (-1.1,3.7) node[left]{vacuum};
\draw[thick] (0,4) ++(0:0.1cm) arc (0:180:0.1cm);
% Labels for height
\draw[<->] (0.5,3) -- (0.5,-0.2) node[midway,right]{h};
% Add some text labels
\node at (0,-1.5) {mercury reservoir};
\end{tikzpicture} 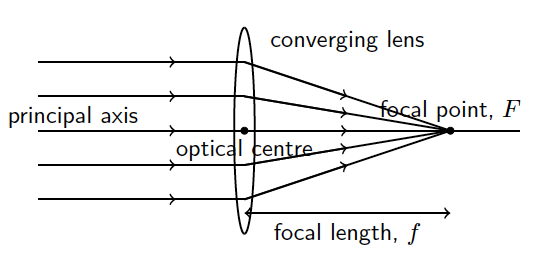
\begin{tikzpicture}
% Draw principal axis
\draw[thick] (-5,0) -- (2,0) node at (-4.5,0.2) {principal axis};
% Draw the lens
\draw[thick] (-2,-1.5) arc[start angle=270, end angle=90, x radius=0.15cm, y radius=1.5cm];
\draw[thick] (-2,1.5) arc[start angle=90, end angle=270, x radius=-0.15cm, y radius=1.5cm];
% Draw the focal points
\node at (1, 0) [above] {focal point, $F$};
\draw[fill] (1, 0) circle [radius=0.05];
\node at (-2, 0) [below] {optical centre};
\draw[fill] (-2, 0) circle [radius=0.05];
% Draw the 3 rays parallel to the principal axis (before hitting the lens)
\draw[thick] (-5,1) -- (-2,1);
\draw[thick] (-5,0.5) -- (-2,0.5);
\draw[thick] (-5,-0.5) -- (-2,-0.5);
\draw[thick] (-5,-1) -- (-2,-1);
\draw[thick, ->] (-4,1) -- (-3,1);
\draw[thick, ->] (-4,0.5) -- (-3,0.5);
\draw[thick, ->] (-4,-0.5) -- (-3,-0.5);
\draw[thick, ->] (-4,-1) -- (-3,-1);
\draw[thick, ->] (-4,0) -- (-3,0);
% Rays converging to the focal point F
\draw[thick] (-2,1) -- (1,0);
\draw[thick] (-2,0.5) -- (1,0);
\draw[thick] (-2,-0.5) -- (1,0);
\draw[thick] (-2,-1) -- (1,0);
\draw[thick, ->] (-2,1) -- (-0.5,0.5);
\draw[thick, ->] (-2,0.5) -- (-0.5,0.25);
\draw[thick, ->] (-2,0) -- (-0.5,0);
\draw[thick, ->] (-2,-0.5) -- (-0.5,-0.25);
\draw[thick, ->] (-2,-1) -- (-0.5,-0.5);
\node at (-0.5, 1.3) {converging lens};
% Focal length
\draw[thick, <->] (-2,-1.2) -- (1,-1.2);
\node at (-0.5, -1.5) {focal length, $f$};
\end{tikzpicture}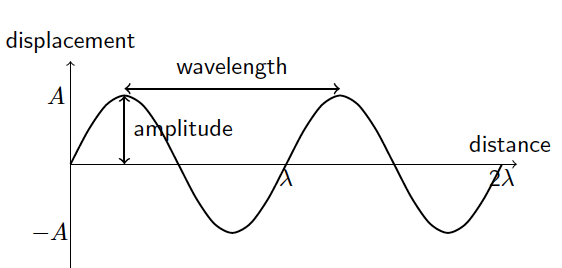
\begin{tikzpicture}
% Draw the wave
\draw[thick, domain=0:6.28, smooth, variable=\x] plot ({\x}, {sin(2*\x r)});
% Draw the x-axis
\draw[->] (0, 0) -- (6.5, 0) node at (6.4,0.3) {distance};
% Draw the y-axis
\draw[->] (0, -1.5) -- (0, 1.5) node[above] {displacement};
% Draw the amplitude arrow
\draw[<->, thick] (0.785, 0) -- (0.785, 1) node[midway, right] {amplitude};
% Draw the wavelength arrow
\draw[<->, thick] (0.785, 1.1) -- (3.925, 1.1) node at (2.355,1.4) {wavelength};
% Label the points
\node at (-0.2, 1) {$A$};
\node at (-0.3, -1) {$-A$};
\node at (3.14, -0.2) {$\lambda$};
\node at (6.28, -0.2) {2$\lambda$};
\end{tikzpicture}Heating and cooling curves are graphical representations that show how the temperature of a substance changes as heat is added or removed over time. They illustrate the behavior of substances as they go through different states—solid, liquid, and gas.
Heating Curve: This curve shows how the temperature of a substance increases as it absorbs heat. The curve typically rises as the substance heats up, with plateaus indicating phase changes, where the substance absorbs energy but its temperature remains constant. Check out the heating curves for water and nitrogen using the drop-down menu.
Cooling Curve: This curve is the opposite of the heating curve. It shows how the temperature decreases as the substance loses heat. Like the heating curve, it also has plateaus where phase changes occur, but this time, the substance releases energy. In addition to water, you can also see the cooling curve for ethanol.
With these ChatGPT-generated interactive graphs, users can change the rate of heat input or released from the substance. They can also read the descriptions that explain the changes in the average PE and KE of the molecules during each process.
A Geiger-Muller (GM) counter is an instrument for detecting and measuring ionizing radiation. It operates by using a Geiger-Muller tube filled with gas, which becomes ionized when radiation passes through it. This ionization produces an electrical pulse that is counted and displayed, allowing users to determine the presence and intensity of radiation.
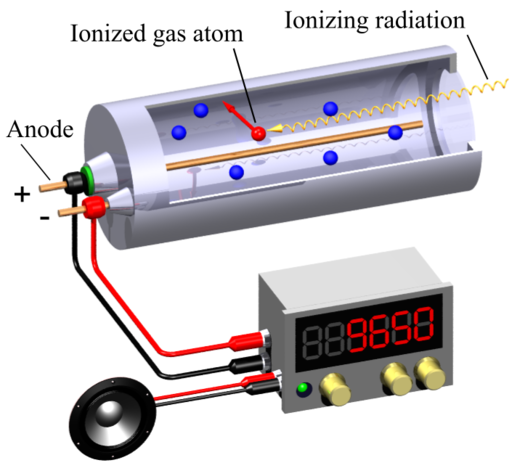
Svjo-2, CC BY-SA 3.0, via Wikimedia Commons
This simulation (find it at https://physicstjc.github.io/sls/gm-counter) allows students to explore the random nature of radiation and the significance of accounting for background radiation in experiments. Here’s a guide to help students investigate these concepts using the simulation.
Exploring Background Radiation
Q1: Set the source to “Background” and start the count. Observe the count for a few minutes. What do you notice about the counts recorded?
Q2: Why is it important to measure background radiation before testing other sources?
Investigating a Banana as a Radiation Source
Q3: Change the source to “Banana” and reset the data. Start the count and observe the readings. How do the counts from the banana compare to the background radiation?
Q4: How do the counts per minute (CPM) for the banana vary over time? Is there a pattern or do the counts appear random?
Exploring a Cesium-137 Source
Q5: Set the source to “Cesium-137” and reset the data. Start the count and observe the readings. How do the counts from Cesium-137 compare to both the background radiation and the banana?
Q6: What do the counts per minute (CPM) tell you about the intensity of the Cesium-137 source compared to the other sources?
Understanding the Random Nature of Radiation
Q7: By looking at the sample counts, can you predict the next count value? Why or why not?
Q8: How can you use the background radiation measurement to correct the readings from the banana and Cesium-137 sources?
Use the quiz below to test your ability to interpret graphs of waves. You can click on a point in the map to read the values.
The codes for this quiz are generated by AI. However, the options and correct answers are rule-based and as such, should not have any errors.
It is able to randomly select from 4 different questions for displacement-distance graphs and 4 others for displacement-time graphs, while randomising the values of amplitude, wavelength and period.
Shared during the East Zone Physics EdTech Workshop 6 Aug 2024
The hands-on workshop for Physics teachers will focus on the use of generative AI to create physics simulations without the user having to write code. The collection of the apps made using AI can be accessed here and the github repository here. This deck of slides is made available here for the participants’ reference. The sample prompts that we will be using can be found at the bottom of this page.
The sample app that we hope the participants can produce will look something like this:
For your convenience, you may refer to the steps below.
STEP 1:
Open ChatGPT or any other GAI (e.g. Claude, CoPilot, Gemini)
STEP 2:
Copy these instructions and paste them into the AI.
- Put all the codes in one page.
- Create a canvas showing a ball dropped from rest from a height and bouncing off the ground using javascript.
- Using the plotly library, plot the graph of velocity versus time for the ball. The time of contact with the ground is negligible.
- Create an input box that allows the user to key in the initial height in metres.
- Create a slider that changes the percentage energy loss after every collision with the ground.
- Create a dropdown menu that changes the vertical axis to velocity or displacement.
- Initialise the animation and graph upon loading. Use a button to start and stop the animation.
STEP 3:
Copy the generated code using the button provided.
STEP 4:
Paste into editor here:
“Run in New Tab” to view and test the app. Download the html file once you are happy with it, or if you would like to add media objects such as images and audio.
STEP 5:
Be prepared to generate 10 or more versions! Repeat STEPS 3-4.
Debugging Options:
- Change the code manually yourself.
- Describe any unexpected behaviour / missing component to AI.
- Ask AI to try a new approach (usually after a few failed iterations).
- To save time, just ask AI to generate the codes that need to be changed. It will tell you where to update.
STEP 6:
Make the app look pretty!
- Optimise for SLS by asking AI to “limit the entire page to a size of max width 580px and max height: 460px”
- Ask AI to beautify the app with styling.
- Ask AI to add image / video / audio files into the code, giving it the filenames, e.g. replace the moving ball with an image of named “ball.png”. This is an example of such an image. You can right-click and “Save as” to save this image file into the same directory as the index.html file.
STEP 7:
To embed into SLS, you will need to copy the code libraries that are used (if any) in a new .js file. The code library is a collection of pre-written code that you can use to perform specific tasks, e.g.
- plotly.js for continously changing graphs
- chart.js for static charts
- papaparse.js for processing csv data
To make a copy of the file,
- Paste the link to the script on browser e.g. https://cdn.plot.ly/plotly-latest.min.js
- Save the page using the “Save as” option in the browser and place the file in the same directory as the html file.
- Rename the path to the file in this way:

STEP 8:
Download as HTML.
Save file as index.html. This is important for SLS packages as it will automatically load the index.html file by default.
STEP 9:
Zip all the files and upload the zip file into SLS component. Follow the user guide on how to do so: https://www.learning.moe.edu.sg/teacher-user-guide/author/html5-content-development/#uploading-a-html5-zip-file-in-sls
