GeoGebra

16 July

Non-Uniform Vertical Circular Motion

Seng Kwang Tan 06 Motion in a Circle, Demonstrations, GeoGebra 0 Comments

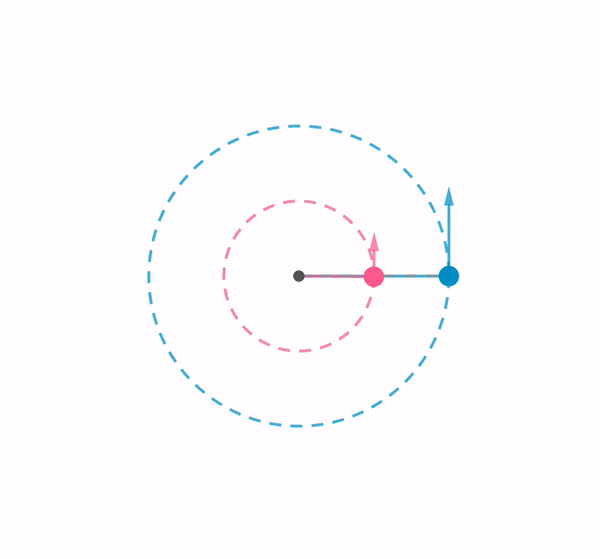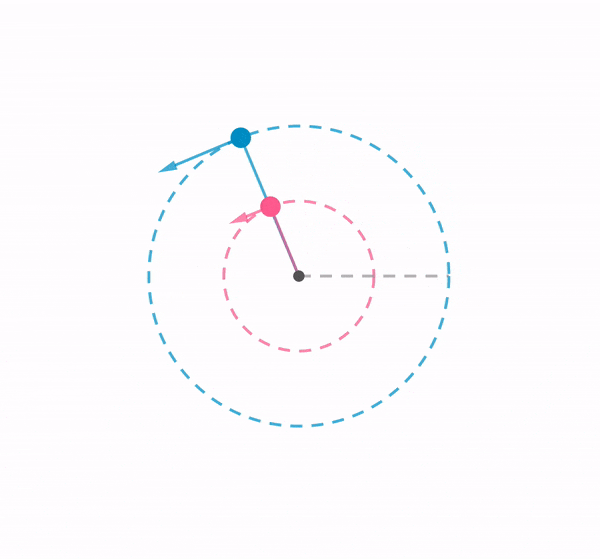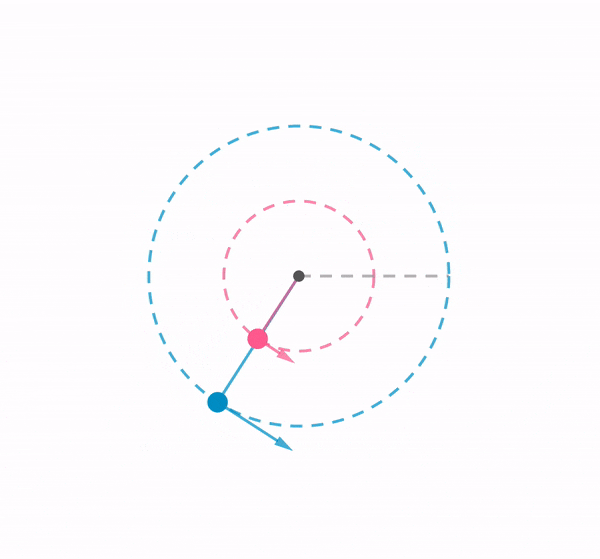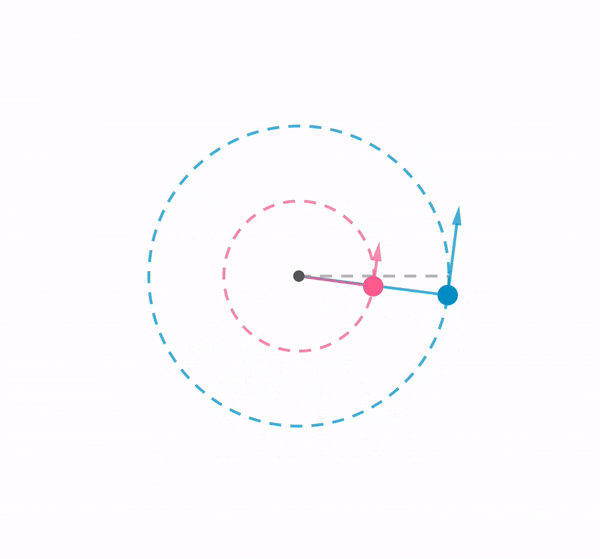
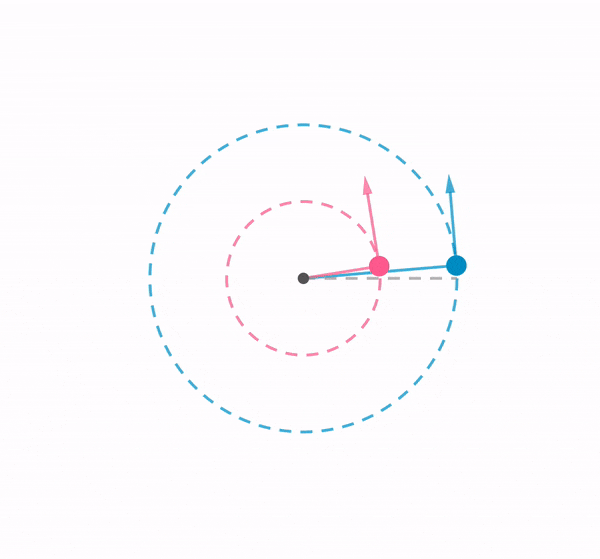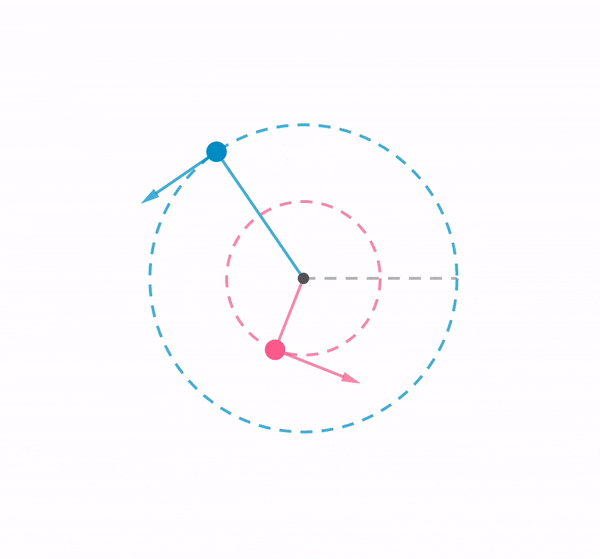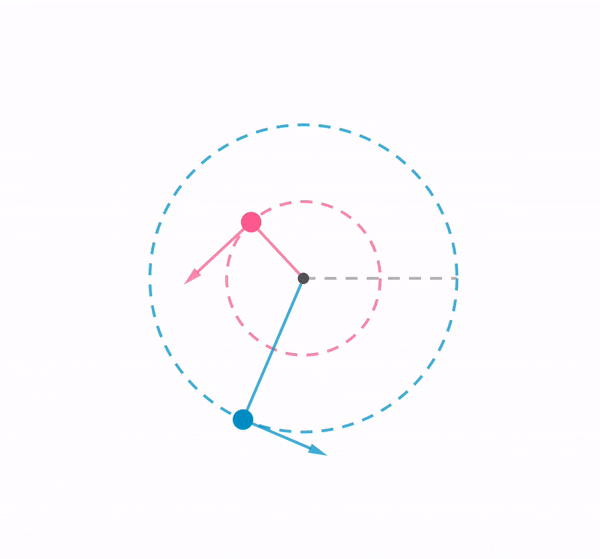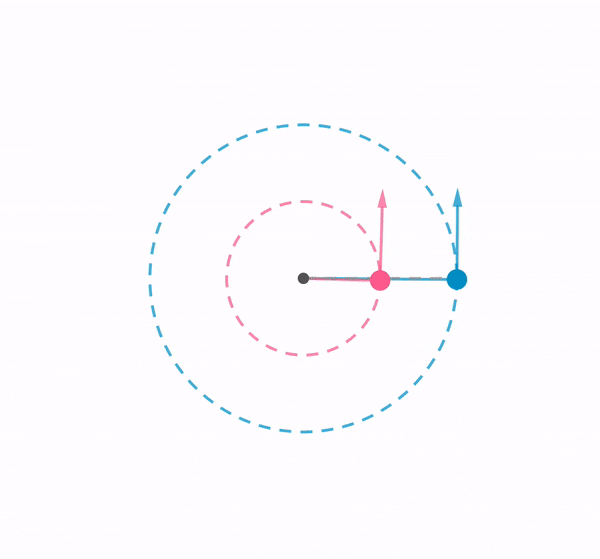
Using a chain of rubber bands, I swung a ball around in a vertical loop. This demonstration shows how the tension in an elastic band changes according to the position of the ball, by referring to the length of the elastic band.

Securing the elastic band to the ball with a shoelace

When the ball of mass $m$ is at the bottom of the loop, the centripetal force is given by the difference between tension $T_{bottom}$ and weight $mg$, where $T_{bottom}$ varies depending on the speed of the ball $v_{bottom}$ and the radius of the curvature $r_{bottom}$.

$T_{bottom} – mg = \dfrac{mv_{bottom}^2}{r_{bottom}}$

When the ball is at the top of the path, it is given by

$T_{top} + mg = \dfrac{mv_{top}^2}{r_{top}}$

As the weight is acting in the same direction to tension when the ball is at the top, a smaller tension is exerted by the elastic band to maintain a centripetal force. Therefore , $T_{bottom} > T_{top}$.

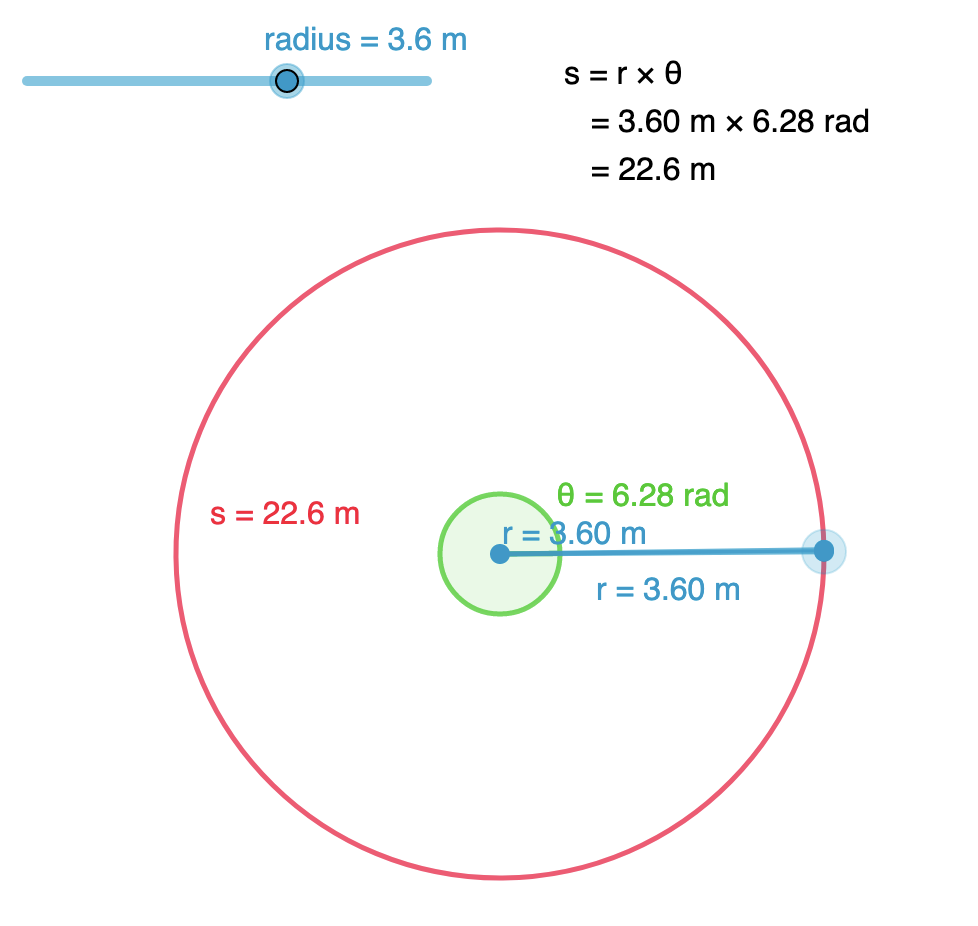
The GeoGebra app below shows a simpler version of a vertical loop – a circular path with a fixed radius $r$. Consider a ball sliding around a smooth circular loop. The normal contact force varies such that

$N_{bottom} = \dfrac{mv_{bottom}^2}{r} + mg$

$N_{top} = \dfrac{mv_{top}^2}{r} – mg$

It can be shown that the minimum height at which the ball must be released in order for it to complete the loop without losing contact with the track is 2.5 times the radius of the frictionless circular track.

If we were to consider the rotational kinetic energy required for the ball to roll, the required initial height will have to be 2.7 times the radius, as shown in the video below:

Many thanks to Dr Darren Tan for his input. Do check out his EJSS simulation of a mass-spring motion in a vertical plane, which comes with many more features such as the ability to vary the initial velocity of the mass, graphs showing the variation of energy and velocity, as well as an option for a mass-string motion as well.

12 July

Escape Velocity

Seng Kwang Tan 07 Gravitation, GeoGebra 0 Comments

Using the GeoGebra app above, I intend to demonstrate the relationship between total energy, kinetic energy and gravitational potential energy in a rocket trying to escape a planet’s gravitational field.

By changing the total energy of the rocket, you will increase the initial kinetic energy, thus allowing it to fly further from the surface of the planet. The furthest point to which the rocket can fly can be observed by moving the slider for “distance”. You will notice that the furthest point is where kinetic energy would have depleted.

Gravitational potential energy of an object is taken as zero at an infinite distance away from the source of the gravitational field. This means gravitational potential energy anywhere else takes on a negative value of $\dfrac{-GMm}{r}$. Therefore, the total energy of the object may be negative, even after taking into account its positive kinetic energy as total energy = kinetic energy + gravitational potential energy.

The minimum total energy needed for the rocket to leave the planet’s gravitational field is zero, as that will mean that the minimum initial kinetic energy will be equal to the increase in gravitational potential energy needed, according to the equation $\Delta U = 0 – (-\dfrac{GMm}{R_P})$, where $R_P$ is the radius of the planet.

Since $\dfrac{1}{2}mv^2 = \dfrac{GMm}{R_P}$, escape velocity, $v = \sqrt{\dfrac{2GM}{R_P}}$.

29 May

Template for self-assessment questions

Seng Kwang Tan GeoGebra 0 Comments

Here is a template that I might use to generate questions for students’ self-assessment in future. Based on a query that one of the participants in a GeoGebra online tutorial asked about generating random questions for simple multiplication for lower primary students.

The online tutorial was conducted by some teachers in the Singapore MOE GeoGebra community to share how GeoGebra could be used to create resources for home-based learning.

24 May

Angular velocity

Seng Kwang Tan 06 Motion in a Circle, GeoGebra 0 Comments

This GeoGebra app shows how angular velocity ω is the rate of change of angular displacement (i.e. $\omega=\dfrac{\theta}{t}$) and is dependent on the speed and radius of the object in circular motion (i.e. $v=r\omega$).

Students can explore the relationships by doing the following:

Keeping r constant and varying ω.

Keeping ω constant and varying r.

Keeping v constant by varying r and ω.

24 May

Angular displacement

Seng Kwang Tan 06 Motion in a Circle, GeoGebra 0 Comments

This GeoGebra app shows the relationship s = rθ.

One activity I get students can do is to look at the value of θ when the arc length s is equal to the radius r. This would give the definition of the radian, which is the angle subtended at the centre of a circle by an arc equal in length to its radius.

Mathematics defines the constant π as the ratio of a circle’s circumference to its diameter. This can also be shown in the app, although you need to drag the moving point to a point just short of one full revolution.

08 May

Creating a simple interactive using GeoGebra

Seng Kwang Tan GeoGebra 0 Comments

While preparing to share with some fellow teachers in Singapore about the use of GeoGebra in Physics, I came up with a set of simple instructions to create an interactive, while introducing tools such as sliders, checkboxes (along with boolean values) and input boxes. Download it here.

You should be able to follow the instructions in the pdf document above and make a simple interactive applet yourself too. The outcome of the interactive applet will be like this:

Embedding GeoGebra into SLS

The following instructions are added on 19 Nov 2024 to update the screens available in SLS.

To embed a GeoGebra app into the Singapore Student Learning Space or any other LMS that supports iframe embedding, note the following:

The size of the interactive should be able to fit a mobile device. I suggest 640px width and 480px height for interactives meant for the Singapore Student Learning Space (SLS). To change the dimensions, go to the page of the specific interactive you want to embed and click on the “more” button (3 dots in a vertical row). Click on “Edit Activity” as shown below.

Next, click on the pencil icon to show “Advanced Settings”

Edit the width and height as required.

Click “Done” and “Save”

To get the embedding codes, go to the “more button” again (see above) and select “Details”.

Click on “Share” and select the “</>Embed” tab.

Copy the iframe embed code and paste it into SLS or your preferred LMS.

In SLS, select “Text/Media” and “Website” to insert the code.