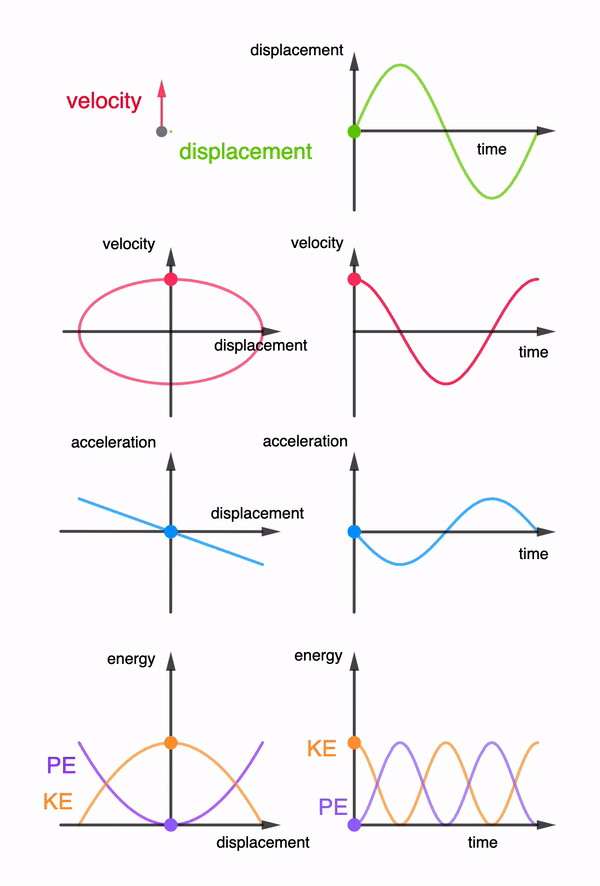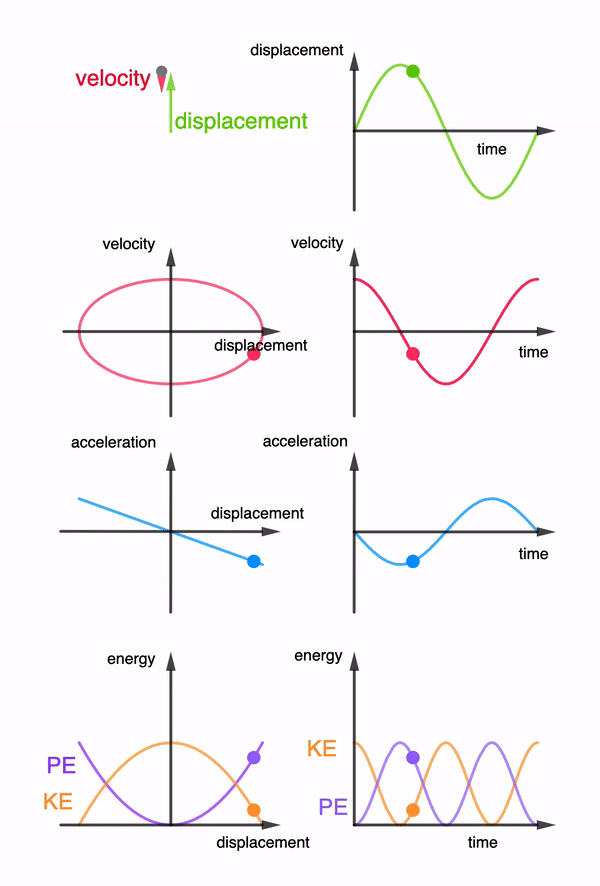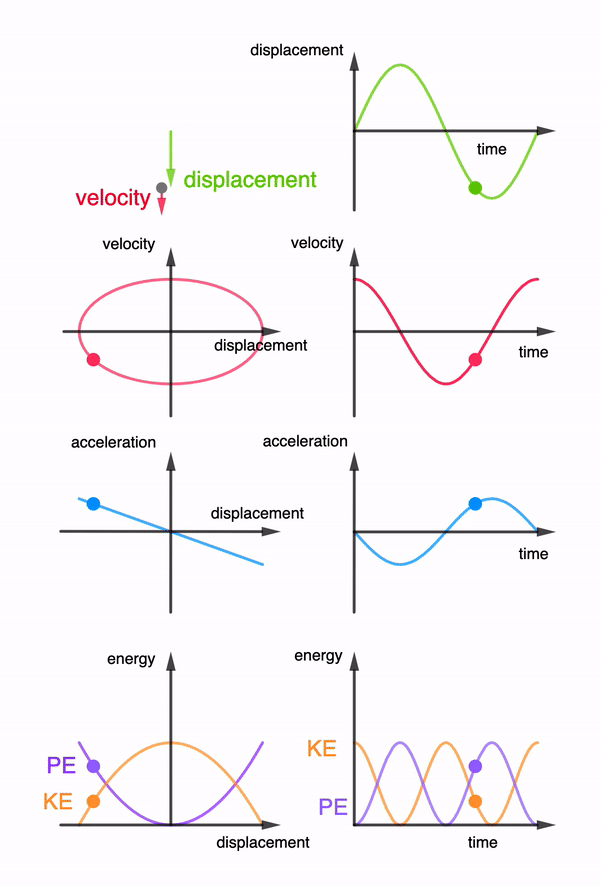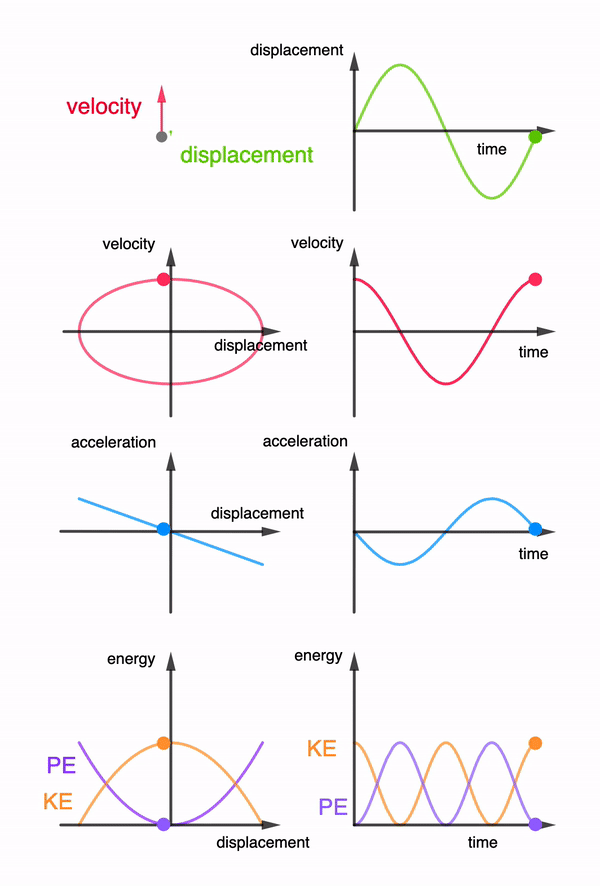
The concept of root-mean-square values for Alternating Currents is challenging if students are to relate the I-t graph with the Irms value directly.
They have to be brought through the 3 steps before arriving at the Irms value. This interactive applet allows them to go through step by step and compare several graphs at one time to see the relationship.
Through the interaction, students might be asked to observe that the Irms value is never higher than the peak Io.
For a complete sinusoidal current:
For a diode-rectified current:
In comparing the Irms of both currents, students can be asked to consider why the ratio of the values is not 2:1 or any other value, from energy considerations.
Worked on this earlier as I am the lead lecturer for this JC2 topic and am trying to integrate useful elements of blended learning. Do let me know in the comments if you have ideas or feedback that you would like to share.