The first of two apps on Phase Difference allows for interaction to demonstrate the oscillation of two different particles along the same wave with a variable phase difference.
The second shows two waves also with a phase difference.
In both cases, the phase difference $\Delta\phi$ can be calculated with
where $\Delta x$ is the horizontal distance between the two particles or the horizontal distance between the two adjacent identical particles (one from each wave) and $\lambda$ is the wavelength of the waves.
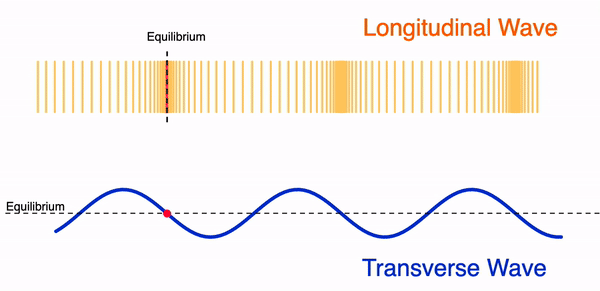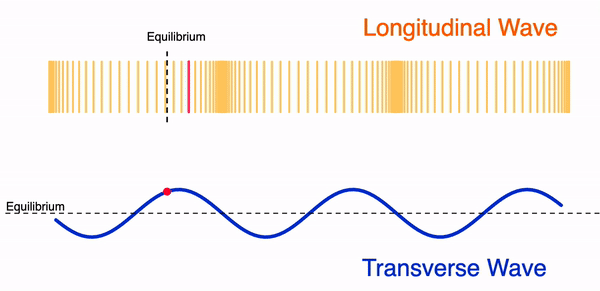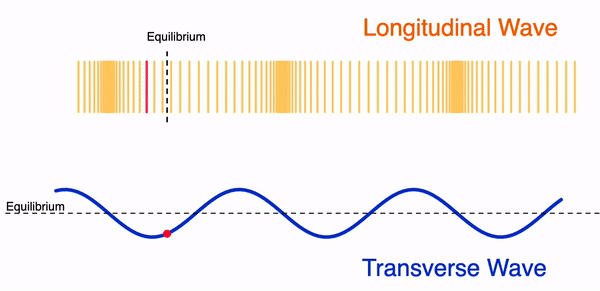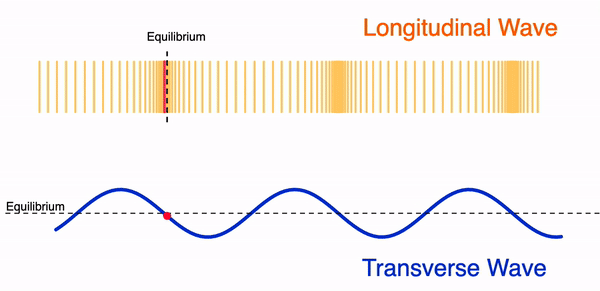
I modified Tom Walsh’s original GeoGebra app to add a moveable single oscillating particle for students to observe its movement along a longitudinal wave and a transverse wave.
The app can also be used to show how the displacement of a particle in a longitudinal wave can be mapped onto a sinusoidal function, similar to the shape of a transverse wave. For example. a displacement of the particle to the right can be represented by a positive displacement value on the displacement-distance graph.
You can choose to select the particle that you want to focus on by using the slider.
This GeoGebra app allows students to observe closely the movement of a particle in a progressive wave, with two possible directions of energy propagation.
In a typical question, students will be asked to predict the next movement of a particle given that a wave is moving left or right. Usually, students will need to imagine the waveform shifting slightly to the left or right in order to figure that out. This app follows the same visualisation technique to identify the subsequent movement of any particle along a wave.
This deck of slides was used today in my sharing session with some colleagues on the use of assessment features in SLS. Sharing it here for anyone who might be interested.
Using a chain of rubber bands, I swung a ball around in a vertical loop. This demonstration shows how the tension in an elastic band changes according to the position of the ball, by referring to the length of the elastic band.
Securing the elastic band to the ball with a shoelace
When the ball of mass $m$ is at the bottom of the loop, the centripetal force is given by the difference between tension $T_{bottom}$ and weight $mg$, where $T_{bottom}$ varies depending on the speed of the ball $v_{bottom}$ and the radius of the curvature $r_{bottom}$.
When the ball is at the top of the path, it is given by
$T_{top} + mg = \dfrac{mv_{top}^2}{r_{top}}$
As the weight is acting in the same direction to tension when the ball is at the top, a smaller tension is exerted by the elastic band to maintain a centripetal force. Therefore , $T_{bottom} > T_{top}$.
The GeoGebra app below shows a simpler version of a vertical loop – a circular path with a fixed radius $r$. Consider a ball sliding around a smooth circular loop. The normal contact force varies such that
$N_{bottom} = \dfrac{mv_{bottom}^2}{r} + mg$
$N_{top} = \dfrac{mv_{top}^2}{r} – mg$
It can be shown that the minimum height at which the ball must be released in order for it to complete the loop without losing contact with the track is 2.5 times the radius of the frictionless circular track.
If we were to consider the rotational kinetic energy required for the ball to roll, the required initial height will have to be 2.7 times the radius, as shown in the video below:
Many thanks to Dr Darren Tan for his input. Do check out his EJSS simulation of a mass-spring motion in a vertical plane, which comes with many more features such as the ability to vary the initial velocity of the mass, graphs showing the variation of energy and velocity, as well as an option for a mass-string motion as well.
Using the GeoGebra app above, I intend to demonstrate the relationship between total energy, kinetic energy and gravitational potential energy in a rocket trying to escape a planet’s gravitational field.
By changing the total energy of the rocket, you will increase the initial kinetic energy, thus allowing it to fly further from the surface of the planet. The furthest point to which the rocket can fly can be observed by moving the slider for “distance”. You will notice that the furthest point is where kinetic energy would have depleted.
Gravitational potential energy of an object is taken as zero at an infinite distance away from the source of the gravitational field. This means gravitational potential energy anywhere else takes on a negative value of $\dfrac{-GMm}{r}$. Therefore, the total energy of the object may be negative, even after taking into account its positive kinetic energy as total energy = kinetic energy + gravitational potential energy.
The minimum total energy needed for the rocket to leave the planet’s gravitational field is zero, as that will mean that the minimum initial kinetic energy will be equal to the increase in gravitational potential energy needed, according to the equation $\Delta U = 0 – (-\dfrac{GMm}{R_P})$, where $R_P$ is the radius of the planet.
Since $\dfrac{1}{2}mv^2 = \dfrac{GMm}{R_P}$, escape velocity, $v = \sqrt{\dfrac{2GM}{R_P}}$.
