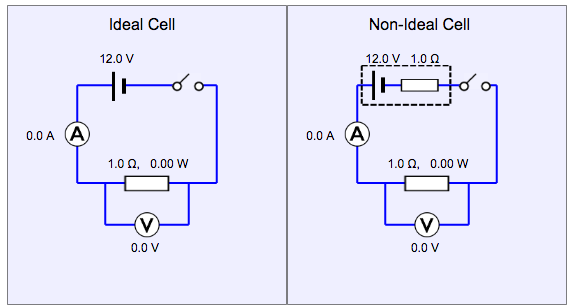
I’ve created this simulation to demonstrate the effect of an internal resistance due to a cell on the potential difference and current of an external load.
One can also vary the internal resistance and external resistance to observe the maximum power theorem. The theorem states that for a given finite internal resistance, one can obtain the maximum external power only when the resistance of the load is equal to the internal resistance of the source.
https://ejss.s3.ap-southeast-1.amazonaws.com/internalresistance_Simulation.xhtml

