30 September

06. Motion in a Circle

Seng Kwang Tan Subject Content 0 Comments

[accordions autoHeight=’true’]

[accordion title=”1. Rotational Kinematics”]

  • Angular displacement $$\theta$$ is defined as the angle an object turns with respect to the centre of a circle. $$\theta=\dfrac{s}{r}$$ where s is the arc and r is the radius of the circle.
  • One radian is the angular displacement when the arc length is equal to the radius of the circle.
  • Angular velocity $$\omega$$ is defined as the rate of change of angular displacement. $$\omega=\dfrac{d\theta}{dt}$$
  • For motion in a circle of fixed radius, $$\omega=\dfrac{d\theta}{dt}=\dfrac{d(\dfrac{s}{r})}{dt}=\dfrac{1}{r}\dfrac{ds}{dt}=\dfrac{v}{r}$$. Thus $$v=r\omega$$.
  • Average angular velocity in one cycle. $$\omega=\dfrac{2\pi}{T}=2\pi f$$ where T is the period and f is the frequency.

[/accordion]

[accordion title=”2. Centripetal Force”]

  • Centripetal acceleration $$a=\dfrac{v^2}{r} = r\omega^2$$.
  • Centripetal force $$F =\dfrac{mv^2}{r} = mr\omega^2$$.

[/accordion]

[accordion title=”3. Uniform Circular Motion”]

For a body in uniform circular motion, there is a change in velocity as the direction of motion is changing. This requires an acceleration that is perpendicular to the velocity and directed towards the centre of circle. This acceleration is provided by a centripetal force. A resultant force acting on a body toward the centre of a circle provides the centripetal force.

[/accordion]

[accordion title=”4. Non-Uniform Circular Motion”]

Learn how to solve problems on circular motions of conical pendulum, cyclist, car, aircraft, swinging a pail etc.

[/accordion]

[/accordions]

26 September

05. Work, Energy and Power

Seng Kwang Tan Subject Content 0 Comments

[accordions autoHeight=’true’]

[accordion title=”1. Work Done”]

  • Work done W is defined as the product of the force and the displacement made in the direction of the force.
    • For a constant force F acting in same direction as the displacement s: W = F . s
    • If $$\theta$$ is the angle between F and s:  $$W = F\cos\theta\cdot s$$

work done

  • Work done = Area under F-s graph.

work done area under graph

 
[/accordion]

[accordion title=”1.1 Work Done on a Spring”]

  • Work done in stretching a spring = area under F-x graph = ½ Fx = ½ kx2


work done by spring

 
[/accordion]

[accordion title=”1.2 Work Done by a Gas”]

  • Work done by expanding gas = area under P-V graph = $$\int P.dV$$

work done by gas

[/accordion]

[accordion title=”2. Kinetic Energy”]

  • Kinetic energy is the energy of a body by virtue of its motion.
  • Derive kinetic energy: W = F.s = ma.s = m ½(v2 – u2)

[/accordion]
[accordion title=”3. Potential Energy”]

  • Potential energy is the energy of a body by virtue of it position.
  • Gravitational Potential Energy near Earth’s surface: $$E_p = mgh$$

gravitational potential energy

[/accordion]

[accordion title=”4. Conservation of Energy”]

  • The Principle of Conservation of Energy states that energy can neither be created nor destroyed in any process. It can be transformed from one form to another, and transferred from one body to another but the total amount remains constant.
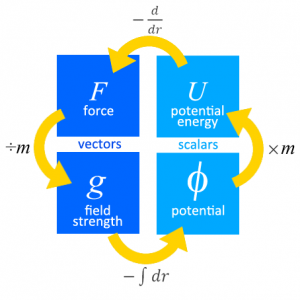
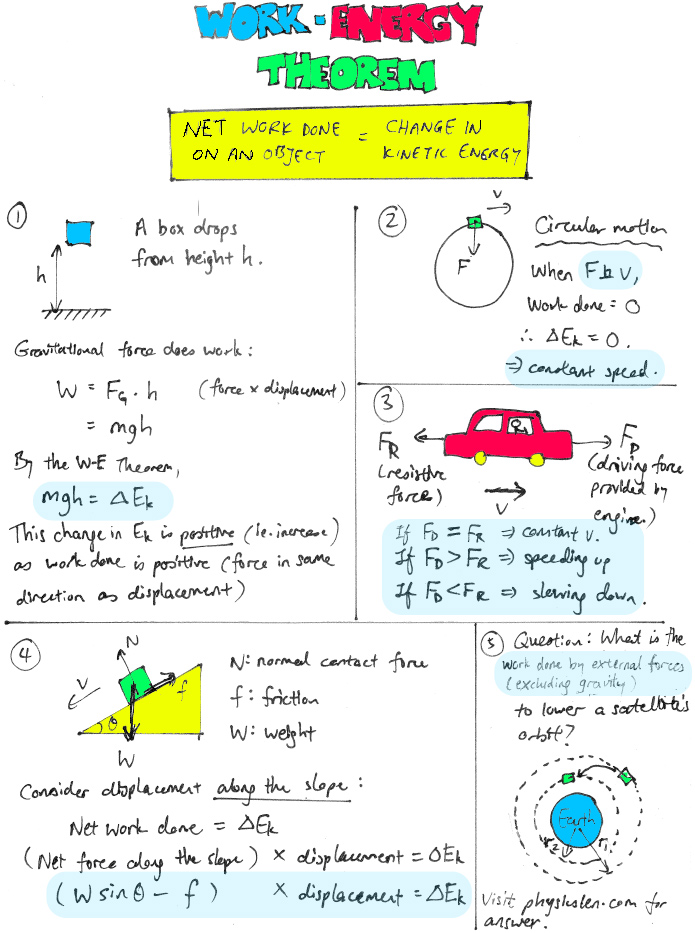
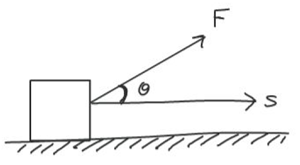
  • The Work-Energy Theorem states that the net work done by external forces acting on a particle is equal to the change in mechanical energy of the particle. i.e. $$W=\Delta E_k+\Delta E_p$$
  • Force $$F =-\dfrac{dU}{dx} = -\text{(gradient of Potential Energy vs displacement graph)}$$

[/accordion]

[accordion title=”5. Power”]

  • Power is work done per unit time
  • Instantaneous Power: $$P = \dfrac{dW}{dt} = F \dfrac{ds}{dt} = F v$$,
  • Average Power: $$<P> = \dfrac{W}{t} = F <v>$$

[/accordion]

[accordion title=”6. Efficiency”]

  • Efficiency $$\eta= \dfrac{E_{output}}{E_{input}}\times 100 \% \text{ or} \dfrac{P_{output}}{P_{input}}\times100\%$$

[/accordion]
[/accordions]

25 September

Who Wants to be a Base Unit?

Seng Kwang Tan 01 Measurement, Games 0 Comments

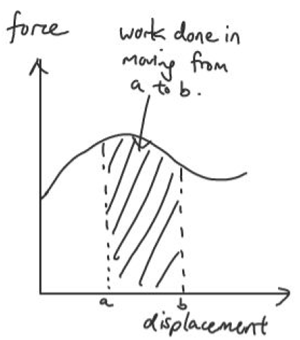
This is a game that I play with my classes in the beginning of the course after they have attended the first lecture on base units. It serves as an ice-breaker since this is usually when I first meet them, as well as a recap of what they have learnt.

The rules are stated in the slideshow.

1. Each student is assigned a base unit out of 3 possible ones, kg, m, s. Note that the other 4 base units, A, mol, K and cd are not given because they will be covered in later topics.
2. For a class of 25, the following distribution is recommended:
    a. kg – 5
    b. m – 10
    c. s – 10
3. Students will be asked to form groups when shown a Physical Quantity. Those with a negative power, e.g. the two “seconds” in kg m s–2, will have to sit/squat down.
4. Students who did not form a group will be ousted and the last few left in the game will win prizes.

Download Measurement Game

19 September

P6 Science Question on Light Bulb

Seng Kwang Tan Blog, Featured 0 Comments

This picture has been making its way around the internet. This is a Primary 6 Science question that has a questionable answer. As teachers, there are times when we make mistakes in crafting answers for a multiple-choice question. Good thing there is often a fail-safe in the form of our colleagues who would help each other vet the questions we set. Sometimes, despite all effort, mistakes are made such as this

Primary 6 Science Question on Light Bulb

The story according to the person who posted this:

This P6 science question is taken from a paper that is set by a local brand name primary school. The majority of the students who took this test gave the answer as (4). The science teacher insisted that the answer is (2). The reason given was that sentence D should be interpreted to mean that only light energy is given off when an electric current passes through it.

The children, as well as many other adults who are well versed in the English language, unanimously agreed that the students were correct to interpret the sentence as meaning that the bulb will give off light energy (though it does not rule out other forms of energy) only if an electric current passes through it (so if there is no electric current, the bulb will not give off light energy.

The HOD called to clarify that her teacher (and therefore the dept) is correct. She apparently said that there is nothing wrong with the statement, and that it is not meant to be read in an ‘English’ way, but rather in a ‘scientific’ way. She then proceeded to read the sentence aloud, pausing after the word ‘only’. When it was pointed out to her that there is a need for a comma after ‘only’ if it is to be read with a pause, she insisted that that was the ‘scientific’ way of reading the sentence, and went on to qualify that laymen would not be able to distinguish between the scientific reading and the English reading, but that the students, having studied the subject for four years, were expected to tell the difference. According to her, this would set the A* students apart from the A students.

Since when our English language developed a ‘scientific’ dialect?! And if you cannot apply standard English language rules to reading the questions of a paper set in English, then perhaps we need to clarify that the paper is written in Scientific-English instead? What kind of nonsense is this?

Many netizens have condemned the answer which was given by the teacher as (2) instead of (4), what made matters worse was the defence given by the HOD. I agree that the statement D could be better phrased as “It gives off only light energy when an electric current passes through it”, therefore making it a false statement and hence, not part of the answer.

This incident reminds us of the need to be careful in the way we phrase our questions, often re-reading them to see if they could be misinterpreted or if they could be made clearer.