15 August

Introducing Delight! An Educational Board Game on Current Electricity

Seng Kwang Tan 15 DC Circuits, Featured, Games, IP4 12 DC Circuits, IP4 13 Practical Electricity, Teaching Resources 0 Comments

Delight - Physics board game on electricity

Download Now

Creative Commons License
Delight by Tan Seng Kwang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.

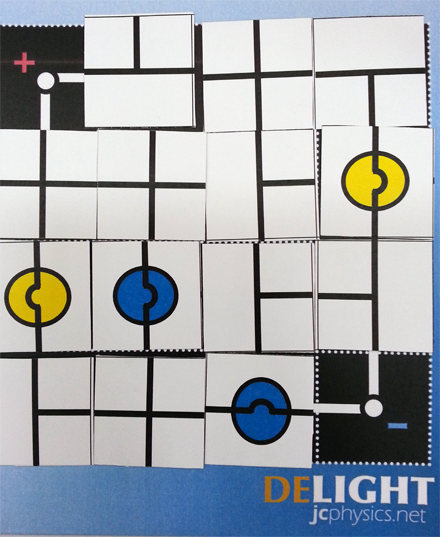
An educational board game for 2 or any even number of players (in 2 teams) based on the concepts of current electricity. Targeted at high school / junior college physics students, Delight is a fun way of practising the use of physics concepts such as

  1. electrical power $$P=\frac{V^2}{R}$$
  2. the potential divider rule.
  3. wires bypassing a device short-circuits it.

This game can be easily printed on A4 paper and the game pieces can be cut up for use.

Game Play

  1. This game is meant for 2 players or 2 teams of players. Each player/team has the following tiles:
    • 2 x light bulbs
    • 3 x T-shaped wires
    • 2 x crossed wires
  2. The players will take turns to place the tiles on the board.
  3. Each new tile must have at least one wire connected to an existing wire on the board.
  4. The game will end when the last tile has been placed on the board.
  5. The person with the brightest bulb will win.In the event that there is an equal number of opposing bulbs of the same brightness, it will be considered a tie. If there are three bulbs of the same brightness, the one with two of these bulbs wins.

Test Yourself: Who is the winner for the games below?

GAME 1

delightend

GAME 2

gameplay2

 

 

 

Conditions for Using this Game

  1. Anyone can print and use this game for free as long as it is for educational or personal use. Any other reproduction or republishing of this material, in hard copy or electronic form, without written permission, is prohibited.
  2. If you would like to make a suggestion or an enquiry, please leave a comment below.
30 July

17. Electromagnetic Induction

Seng Kwang Tan Subject Content

How emf is induced

Electromagnetic Induction and its Effects

To explain a phenomenon that happens due to Electromagnetic Induction, we can use an acronym CFILE to structure our answer.

C stands for cutting of flux or changing of flux linkage. This is necessary for electromagnetic induction to happen. When a wire is pulled through a magnetic field perpendicular to it, it is said to be cutting the field lines. When a magnet enters a coil of wires, we can say that the magnetic flux linkage is increasing.

F stands for Faraday’s law, which states that the induced e.m.f. in a circuit is directly proportional to the rate of change of flux-linkage or to the rate of cutting of magnetic flux.

I stands for an induced current. However, do note that this is only possible if there is a closed circuit or a path for the current to flow.

L stands for Lenz’s law, which states that the direction of the induced e.m.f. is such that it tends to oppose the flux change causing it, and does oppose it if induced current flows. 

E stands for effect. This is really just stating how an induced current or Lenz’s law causes the phenomenon in question.

28 July

18. Alternating Currents

Seng Kwang Tan Subject Content
  • The root-mean-square value of an alternating current is equivalent to the steady direct current that would dissipate heat at the same rate as the alternating current in a given resistor.
  • For a sinusoidal source,
    (a) the root mean square value of the current is given by $$I_{rms}=\frac{I_o}{\sqrt{2}}$$.
    (b) the mean or average power < P > absorbed by a resistive load is half the maximum power.
    $$<P>=\frac{1}{2}P_o=\frac{1}{2}{I_o}{V_o}=\frac{1}{2}{I_o}^2R =\frac{V_o^2}{2R}$$.
  • An a.c. transformer is a device for increasing or decreasing an a.c. voltage. It consists of a primary coil of Np turns and voltage Vp and secondary coil of Ns turns and voltage Vs wrapped around an iron core.
  • For an ideal transformer (assuming no energy is lost), the following equation is obeyed
    $$\frac{N_s}{N_p}=\frac{V_s}{V_p}=\frac{I_p}{I_s}$$.
  • Power loss in the transmission lines is minimized if the power is transmitted at high voltages (i.e. low currents) since $$P_{loss}=I^2R$$ where I is the current through the cables and R is the resistance of the cables.
  • The equation $$P=\frac{V^2}{R}$$ is often mistakenly used to suggest that power lost is high when voltage of transmission is high. In fact, V refers to the potential difference across the cables, which often have but a fraction of the overall resistance through which the current passes.