Students are often confused about the forces in drawing free-body diagrams, especially so when they have to consider the different parts of multiple bodies in motion.
Two-Body Motion
Let’s consider the case of a two-body problem, where, a force F is applied to push two boxes horizontally. If we were to consider the free-body diagram of the two boxes as a single system, we only need to draw it like this.
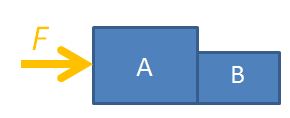
For the sake of problem solving, there is no need to draw the normal forces or weights since they cancel each other out, so the diagram can look neater. Applying Newton’s 2nd law of motion, $F=(m_A+m_B) \times a$, where $m_A$ is the mass of box A, $m_B$ is the mass of box B, F is the force applied on the system and a is the acceleration of both boxes.
You may also consider box A on its own.
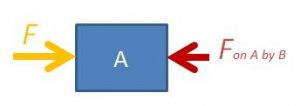
The equation is $F-F_{AB}=m_A \times a$, where $F_{AB}$ is the force exerted on box A by box B.
The third option is to consider box B on its own.

The equation is $F_{BA}=m_B \times a$, where $F_{BA}$ is the force exerted on box B by box A. Applying Newton’s 3rd law, $F_{BA}=F_{AB}$ in magnitude.
Never Draw Everything Together
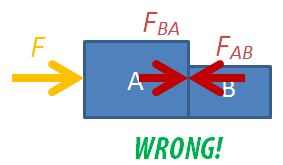
NEVER draw the free-body diagram with all the forces and moving objects in the same diagram, like this:
You will not be able to decide which forces acting on which body and much less be able to form a sensible equation of motion.
Interactive
Use the following app to observe the changes in the forces considered in the 3 different scenarios. You can vary the masses of the bodies or the external force applied.
Multiple-Body Problems
For the two-body problem above, we can consider 3 different free-body diagrams.
For three bodies in motion together, we can consider up to 6 different free-body diagrams: the 3 objects independently, 2 objects at a go, and all 3 together. Find the force between any two bodies by simplifying a 3-body diagram into 2 bodies. This trick can be applied to problems with even more bodies.