Polarization Using Sunglasses and a Computer Screen

Using a pair of polarizing sunglasses, you can demonstrate the effects of polarization together with a computer screen which is also polarizing. When the axes of polarization of the two polarizing screens are rotated, the brightness alternates between bright and dark.

Light coming from a computer screen is usually polarized. In the video below, when polarized light passes through another polarizer, the intensity of the light is given by Malus’ law:

$$I=I_{o}co{s}^2\theta$$

where $$\theta$$ is the angle between the two axes of polarization and $$I_o$$ is the original intensity of the unpolarized light.

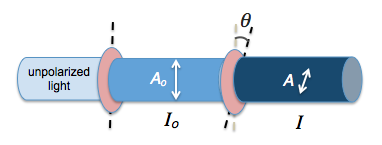
Only the components of electric field vectors in electromagnetic radiation that are parallel to the axis of polarization of a polarizing filter will be permitted through. Those electric field components that are perpendicular to the polarization axis are blocked by the filter.

Hence, the amplitude of a vector A that passes through is given by $$A=A_o\cos \theta$$. Since intensity is proportional to the square of amplitude ($$I\propto A^2$$), we have Malus’ law.

The purpose of having polarizing filters in sunglasses and computer screens is to cut out glare due to light from other sources.