I’ve used the open-source Tracker software, a video analysis and modeling tool built for use in Physics education, for both my IP3 and JC1 classes this year. Thanks to Mr Wee Loo Kang and his team for enthusiastically introducing this software to the physics teachers of Singapore.
For the IP3 cohort, students were tasked to analyse the movement of any sports-related projectile and to relate the variations in displacement, velocity and acceleration to one another in both dimensions. This was a direct transfer task for the topic of two-dimensional kinematics that they were taught in class. Attempts to explain these variations using the idea of forces were encouraged as well, even though that topic has not be formally introduced yet.
For my JC1 class, I explained the specific example of the bouncing ball using the software, which was useful to show the variation in vertical displacement, velocity and acceleration synchronously with the positions of the ball. I used the resources in the Singapore Tracker Digital Library, search for the following directories: 02_newtonianmechanics_2kinematics > trz > Balldropbounce4x.trk.
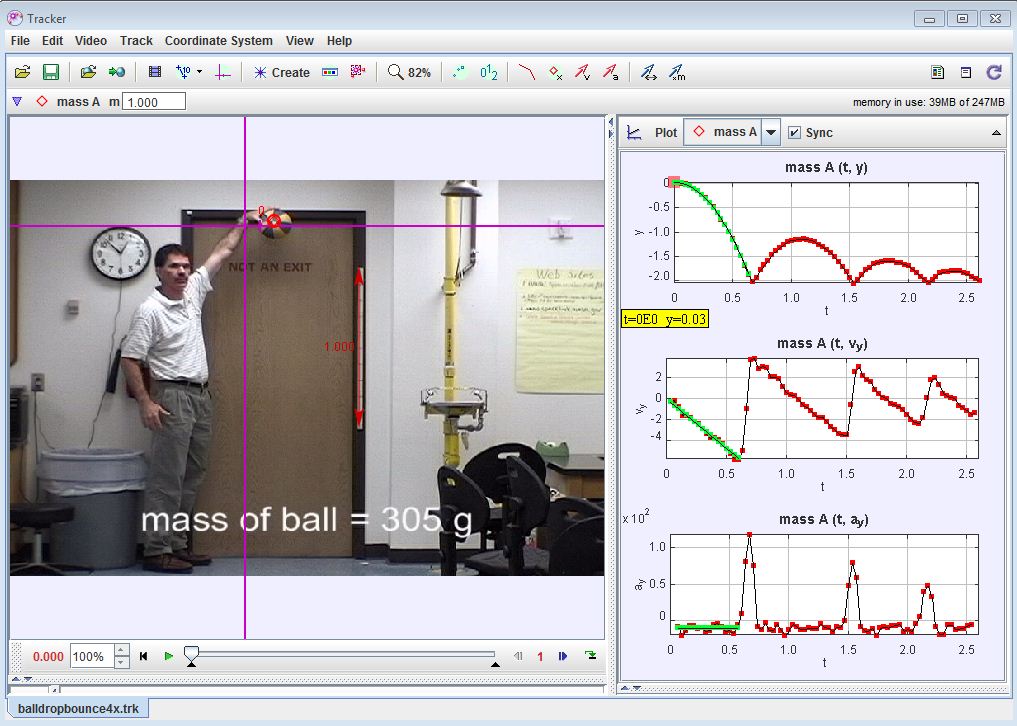
It was easier for students to compare the three stages of the movement, namely
Stage A: the way up,
Stage B: the bounce (during which the ball is in contact with the ground)
Stage C: and the way down.
A series of guiding questions such as the following will be useful:
- Is there a difference between the vertical accelerations in stages A and C?
- What do the gradients in the velocity time graph for stages A, B and C represent?
- Identify the turning point of the ball in all 3 graphs. Notice that the acceleration remains at about 10 m s-2.
- How would the graphs look like if the coordinate system / sign convention is changed such that the displacement is defined as zero at the floor and upward is taken to be positive? The effect of this change can be shown by dragging the axes on the video (the two perpendicular purple lines) to the bottom and rotating the horizontal axis 180o; by dragging the short purple line near the intersection.
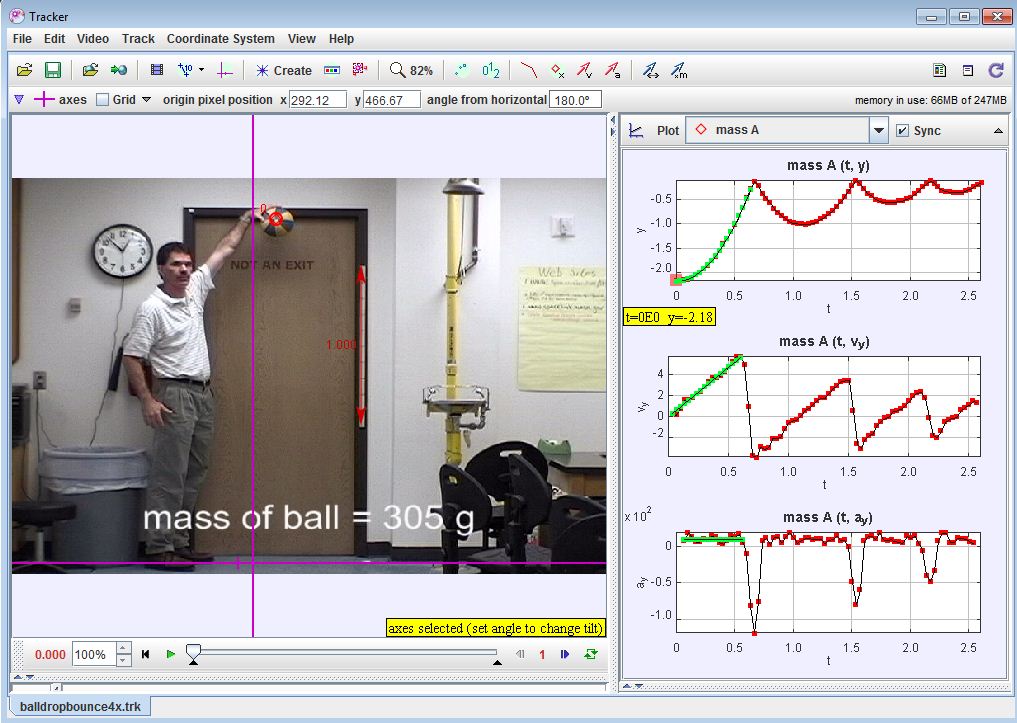
The following video (sorry, no audio) shows the steps to take to do all the above. Just pause it at any point and rewind if you didn’t catch what I did.